题目内容

袋中有5个白球、3个黑球,从中任意摸出4个.其中第一次摸出一个白球,求下列事件发生的概率.

(1)摸出1个或2个黑球;

(2)至少摸出1个黑球.

分析:本题可直接求出.

解:(1)摸出1个或2个黑球的概率为

P=+=.(2)至少摸出一个黑球的概率为P=1=1.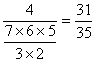

绿色通道

    本题为条件概率,可在摸出一个白球的基础上分类直接求出满足条件的概率.

(专题四)独立性检验

    两个变量之间有无关联,可通过计算χ2的值来说明相关的可能性大小.当χ2＜2.706时两变量无关;当χ2＞2.706时有90%的把握认为两变量相关联;当χ2＞3.841时就有95%的把握认为两变量有关联;当χ2＞6.635时就有99%的把握认为两变量有关联.

练习册系列答案
相关题目
袋中有5个白球，3个黑球，从中任意摸出4个，求下列事件发生的概率：
（1）摸出2个或3个白球；
（2）至少摸出1个白球；
（3）至少摸出1个黑球．
A袋中有5个白球和3个黑球，从其中任取2个球，则取得二球颜色不相同的概率是（　　）
A、0.357B、0.107C、0.646D、0.250
一袋中有5个白球，3个红球，现从袋中往外取球，每次任取一个记下颜色后放回，直到红球出现10次时停止，设停止时共取了ξ次球，则P（ξ=12）等于（　　）
A、C1210（
3
8
）10•（
5
8
）2
B、C119（
3
8
）9（
5
8
）2•
3
8
C、C119（
5
8
）9•（
3
8
）2
D、C119（
3
8
）9•（
5
8
）2
袋中有5个白球，3个黑球，从中任取3个球，则至少有一个白球的概率是（　　）
A、
1
56
B、
55
56
C、
53
55
D、
52
65
袋中有5个白球、3个黑球，从中任意摸出4个，则至少摸出1个黑球的概率是（    ）

A.                B.              C.              D.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网