题目内容
设函数 定义在
定义在 上,
上, ,导函数
,导函数 ,
, .
.
(1)求 的单调区间和最小值;
的单调区间和最小值;
(2)讨论 与
与 的大小关系;
的大小关系;
(3)是否存在 ,使得
,使得 对任意
对任意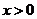 成立?若存在,求出
成立?若存在,求出 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】
【分析】(1)先求出原函数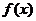 ,再求得
,再求得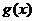 ,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
,然后利用导数判断函数的单调性(单调区间),并求出最小值;(2)作差法比较,构造一个新的函数,利用导数判断函数的单调性,并由单调性判断函数的正负;(3)存在性问题通常采用假设存在,然后进行求解;注意利用前两问的结论.
【解】(1)∵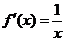 ,∴
,∴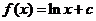 (
(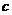 为常数),又∵
为常数),又∵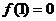 ,所以
,所以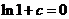 ,即
,即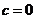 ,
,
∴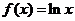 ;
;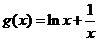 ,
,
∴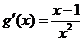 ,令
,令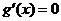 ,即
,即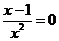 ,解得
,解得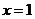 ,
,
当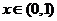 时,
时,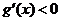 ,
,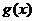 是减函数,故区间在
是减函数,故区间在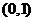 是函数
是函数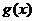 的减区间;
的减区间;
当 时,
时,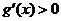 ,
,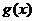 是增函数,故区间在
是增函数,故区间在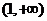 是函数
是函数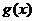 的增区间;
的增区间;
所以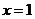 是
是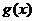 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
所以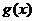 的最小值是
的最小值是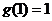 .
.
(2)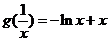 ,设
,设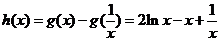 ,
,
则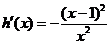 ,
,
当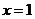 时,
时,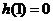 ,即
,即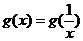 ,
,
当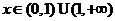 时,
时,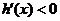 ,
,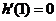 ,
,
因此函数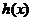 在
在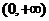 内单调递减,
内单调递减,
当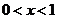 时,
时,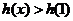 =0,∴
=0,∴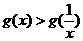 ;
;
当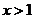 时,
时,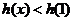 =0,∴
=0,∴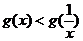 .
.
(3)满足条件的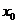 不存在.证明如下:
不存在.证明如下:
证法一 假设存在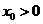 ,使
,使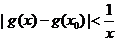 对任意
对任意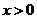 成立,
成立,
即对任意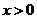 有
有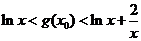 ①
①
但对上述的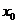 ,取
,取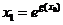 时,有
时,有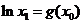 ,这与①左边的不等式矛盾,
,这与①左边的不等式矛盾,
因此不存在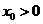 ,使
,使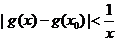 对任意
对任意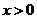 成立.
成立.
证法二 假设存在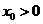 ,使
,使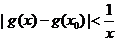 对任意
对任意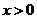 成立,
成立,
由(1)知,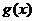 的最小值是
的最小值是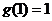 ,
,
又 ,而
,而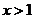 时,
时,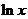 的值域为
的值域为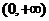 ,
,
∴当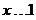 时,
时,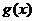 的值域为
的值域为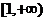 ,
,
从而可以取一个值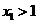 ,使
,使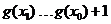 ,即
,即 ,
,
∴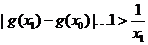 ,这与假设矛盾.
,这与假设矛盾.
∴不存在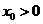 ,使
,使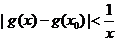 对任意
对任意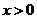 成立.
成立.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
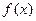 定义在
定义在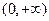 上,
上,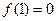 ,导函数
,导函数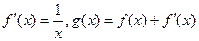
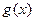 的单调区间的最小值;(Ⅱ)讨论
的单调区间的最小值;(Ⅱ)讨论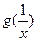 的大小关系;(Ⅲ)是否存在
的大小关系;(Ⅲ)是否存在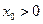 ,使得
,使得 对任意
对任意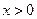 成立?若存在,求出
成立?若存在,求出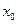 的取值范围;若不存在请说明理由。
的取值范围;若不存在请说明理由。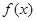 定义在
定义在 上,
上,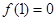 ,导函数
,导函数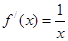 ,
,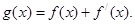
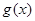 与
与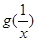 的大小关系;
的大小关系;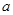 的取值范围,使得
的取值范围,使得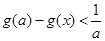 对任意
对任意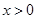 成立.
成立. 定义在
定义在 上,
上, ,导函数
,导函数 ,
, .
. 的单调区间和最小值;(2)讨论
的单调区间和最小值;(2)讨论 的大小关系;
的大小关系;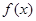 定义在
定义在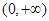 上,
上,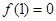 ,导函数
,导函数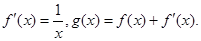
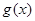 的单调区间和最小值;[来源:学#科#网]
的单调区间和最小值;[来源:学#科#网]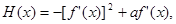 在
在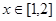 上的最大值。
上的最大值。