题目内容
.(本小题满分12分)设函数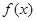 定义在
定义在 上,
上,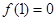 ,导函数
,导函数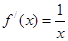 ,
,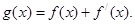
(I)讨论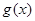 与
与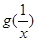 的大小关系;
的大小关系;
(II)求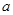 的取值范围,使得
的取值范围,使得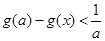 对任意
对任意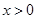 成立.
成立.
【答案】
解:(I)∵ ,∴
,∴ (c为常数),又∵
(c为常数),又∵ ,所以
,所以 ,即
,即 ,∴
,∴ ,∴
,∴ ,
,
令 得
得 ,
,
当x∈(0,1)时, ,
, 是减函数,故(0,1)是
是减函数,故(0,1)是 的单调减区间。
的单调减区间。
当x∈(1,+∞)时, ,
, 是增函数,故(1,+∞)是
是增函数,故(1,+∞)是 的单调递增区间,
的单调递增区间,
因此, 是
是 的唯一极值点,且为极小值点,从而是最小值点,
的唯一极值点,且为极小值点,从而是最小值点,
所以 的最小值为
的最小值为
 ,设
,设 ,则
,则 ,
,
当 时,
时, ,即
,即 .
.
当 时,
时, ,因此,
,因此, 在
在 内单调递减,
内单调递减,
当 时,
时, ,即
,即 ;
;
当 时,
时, ,即
,即
(II)由(I)知 的最小值为1,所以,
的最小值为1,所以, ,对任意
,对任意 成立
成立 ,即
,即 ,从而得
,从而得
【解析】略

练习册系列答案
相关题目