题目内容
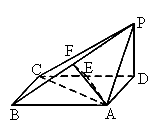
如图，四棱锥PABCD中，底面ABCD为矩形，PD⊥底面ABCD，AD＝PD，E、F分别为CD、PB的中点．求证：EF⊥平面PAB．
答案：略
解析：
解析：
|
证明：如图连结 EP．∵ PD⊥底面ABCD，DE在平面ABCD内，∴ PD⊥DE．又CE=ED，PD=AD=BC．∵ Rt△BCE≌Rt△PDE，∴ PE=BE∵ F为PB中点，∴ EF⊥PB由三垂线定理，得 PA⊥FA．∴在 Rt△PAB中PF=AF，又 PE=BE=EA．∴△ EFP≌△EFA．∴EF⊥FA．∵ PB、FA为平面PAB内的相交直线∴ EF⊥平面PAB
|
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
ABCD的底面是边长为a的正方形，PB⊥面ABCD．
，求这个四棱锥的体积；
．
－
中，底面
底面
，
，．
； 
与平面
所成的角为
，求二面角
－
－
的大小．
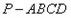三视图中的主视图为边长为
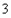的正三角形，俯视图的轮廓为边长为3的正方形。
底面ABCD，E是PC的中点．
∥平面
；
