题目内容
已知两定点A、B距离为8,求到A、B两点距离的平方和是50的动点的轨迹方程.解法一:以A、B两点连线为x轴,线段AB的中垂线为y轴,建立直角坐标系,如图,则A、B两点的坐标分别为A(-4,0)、B(4,0).设P(x,y)为所求曲线上任意一点.?
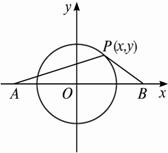
由曲线的几何特征得|PA| 2+|PB| 2=50.?
∴![]() .?
.?
化简上式得x2+y2=9.∴所求轨迹方程为x2+y2=9.
解法二:以A、B两点连线为x轴,A为坐标原点建立直角坐标系,则A(0,0),B(8,0).
设曲线上的动点P(x,y).?
由题意:|PA|2+|PB|2=50,?
即![]() .?
.?
化简得x2+y2-8x+7=0.?
故所求轨迹方程为x2+y2-8x+7=0.
点评:两种解法所得方程不同,这说明建立的直角坐标系不同,所得的曲线方程一般也不相同,且其求解过程也有简有繁,但曲线的形状、大小完全相同.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
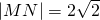 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;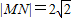 ,l∥AB,如果直线AM和BN的交点C在y轴上;
,l∥AB,如果直线AM和BN的交点C在y轴上;