题目内容
已知函数f(x)满足2f(x)+f
=6x+
，对x≠0恒成立，在数列{an}、{bn}中，a1=1，b1=1，对任意n∈N*，an+1=
,bn+1-bn=
.(1)求函数f(x)的解析式;
(2)求{an}和{bn}的通项公式；
(3)若对任意实数
，总存在自然数k,当n≥k时，bn≥
恒成立，求k的最小值．
(1)2f(x)+f()=6x+
f(x)+2f()=+3x f(x)=3x
(2)∵an+1=
∴
∴数列{
}是以1为首项，2为公差的等差数列,
∴
=1+2(n-1)=2n-1
an=
(n∈N*)
∵bn+1-bn=
=2n-1
bn-bn+1=2(n-1)-1
bn-1-bn-2=2(n-2)-1
…
b3-b2=2×2-1
b2-b1=2-1
上面各式相加，得
bn+1-b1=2[n+(n-1)+…+2+1]-n=n2
bn=(n-1)2+1=n2-2n+2
(3)对任意实数λ∈[0,1]时，bn≥
f(
)恒成立
对任意实数λ∈[0,1]时,
(2n-1)λ+n2-4n+3≥0恒成立.
令g(λ)=(2n-1)λ+n2-4n+3,则g(λ)是一次函数,
∴
对任意实数λ∈[0,1]时，
.
.
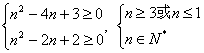∴n≥3或n≤1,n∈N* 故kmin=3.
练习册系列答案
相关题目
,
)时，f(x)=x+sinx,设a=f(1),b=f(2),c=f(3)，则( )
+
+
+
+
的值为_______________．