Question

【题目】已知函数.

（1）讨论函数的单调性；

（2）记，是的导函数，如果是函数的两个零点，且满足，证明：.

Answer 1

【答案】（1）见解析（2）见解析

【解析】分析：（1）取出函数的导数，结合二次函数的性质，通过讨论的范围，求出函数的单调区间，即可；

（2）求出，令，则，根据函数的单调性证明即可．

详解：（1）的定义域为，

.

设，为二次函数，对称轴，且恒过点，

（i）当时,，所以，在上单调递减；

（ii）当时，

令，可得，.

若时， .

当时，，；时，，.所以在上单调递减；在上单调递增.

当时，,.

对任意，，恒成立，所以在上单调递减；

当时，，.

当时，，；时，，.

所以在上单调递减，在上单调递增.

综上，当时，在上单调递减；在上单调递增.

当时， 在上单调递减.

当时，在上单调递减；在上单调递增.

（2），.

将

两式相减，整理得，

即，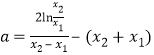

所以

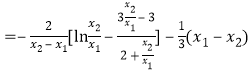
令，，

则，

所以在上单调递减，故

又，所以.