题目内容
已知曲线C：f（x）=x3-x
（Ⅰ）试求曲线C在点（1，f（1））处的切线方程；
（Ⅱ）试求与直线y=5x+3平行的曲线C的切线方程．
（Ⅰ）试求曲线C在点（1，f（1））处的切线方程；
（Ⅱ）试求与直线y=5x+3平行的曲线C的切线方程．
考点：利用导数研究曲线上某点切线方程,直线的一般式方程与直线的平行关系
专题：计算题,导数的概念及应用
分析：（Ⅰ）求出导数，求出切线的斜率和切点，由点斜式写出直线方程；
（Ⅱ）设出切点，求出切线的斜率，由两直线平行的条件得，切点的坐标，应用点斜式方程写出切线方程，并化为一般式方程．
（Ⅱ）设出切点，求出切线的斜率，由两直线平行的条件得，切点的坐标，应用点斜式方程写出切线方程，并化为一般式方程．
解答：
解：（Ⅰ）∵f（x）=x3-x，∴f（1）=0，
求导数得：f'（x）=3x2-1，
∴切线的斜率为k=f'（1）=2．
∴所求切线方程为y=2（x-1），即：2x-y-2=0．
（Ⅱ）设与直线y=5x+3平行的切线的切点为（x0，y0），
则切线的斜率为k=f′(x0)=3x02-1，
又∵所求切线与直线y=5x+3平行，∴3x02-1=5．
解得：x0=±
，
代入曲线方程f（x）=x3-x得：切点为(
，
)或(-
，-
)，
∴所求切线方程为：y-
=5(x-
)或y+
=5(x+
)
即：5x-y-4
=0或5x-y+4
=0．
求导数得：f'（x）=3x2-1，
∴切线的斜率为k=f'（1）=2．
∴所求切线方程为y=2（x-1），即：2x-y-2=0．
（Ⅱ）设与直线y=5x+3平行的切线的切点为（x0，y0），
则切线的斜率为k=f′(x0)=3x02-1，
又∵所求切线与直线y=5x+3平行，∴3x02-1=5．
解得：x0=±
| 2 |
代入曲线方程f（x）=x3-x得：切点为(
| 2 |
| 2 |
| 2 |
| 2 |
∴所求切线方程为：y-
| 2 |
| 2 |
| 2 |
| 2 |
即：5x-y-4
| 2 |
| 2 |
点评：本题主要考查导数的概念及应用：求切线方程，同时考查两直线平行的条件，是一道基础题．
练习册系列答案
相关题目
已知椭圆C方程：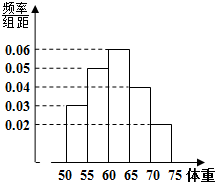
某公司为了了解员工们的健康状况，随机抽取了部分员工作为样本，测量他们的体重（单位：公斤），体重的分组区间为[50，55），[55，60），[60，65），[65，70），[70，75]，由此得到样本的频率分布直方图，如图所示．根据频率分布直方图，估计该公司员工体重的众数是