题目内容
已知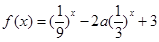
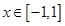
(1)若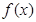 的最小值记为
的最小值记为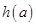 ,求
,求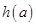 的解析式.
的解析式.
(2)是否存在实数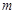 ,
,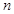 同时满足以下条件:①
同时满足以下条件:①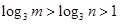 ;②当
;②当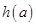 的定义域为[
的定义域为[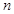 ,
,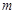 ]时,值域为[
]时,值域为[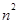 ,
,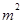 ];若存在,求出
];若存在,求出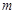 ,
,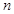 的值;若不存在,说明理由.
的值;若不存在,说明理由.
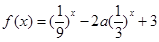
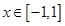
(1)若
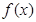 的最小值记为
的最小值记为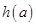 ,求
,求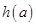 的解析式.
的解析式.(2)是否存在实数
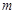 ,
,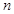 同时满足以下条件:①
同时满足以下条件:①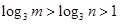 ;②当
;②当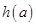 的定义域为[
的定义域为[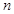 ,
,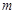 ]时,值域为[
]时,值域为[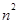 ,
,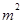 ];若存在,求出
];若存在,求出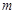 ,
,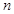 的值;若不存在,说明理由.
的值;若不存在,说明理由.(1)  ;(2) 满足条件的实数m,n不存在.
;(2) 满足条件的实数m,n不存在.
 ;(2) 满足条件的实数m,n不存在.
;(2) 满足条件的实数m,n不存在.试题分析:(1)利用换元法令
 ,可知
,可知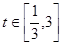 ,原函数化为
,原函数化为 ,利用一元二次函数求最值,可得最小值
,利用一元二次函数求最值,可得最小值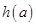 的解析式;(2)由 ①知m>n>3,故
的解析式;(2)由 ①知m>n>3,故 ,由函数的单调性知
,由函数的单调性知12?6m=n2,12?6n=m2 得m+n=6与m>n>3矛盾,故不存在.
解:(1)令
 ,∵
,∵ ∴
∴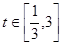 , 1分
, 1分
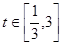 ,对称轴
,对称轴 . 2分
. 2分①

②
 ,
,③
 , 5分
, 5分∴
 7分
7分(2)因为
 在(3,+∞)上为减函数,而m>n>3,
在(3,+∞)上为减函数,而m>n>3,∴
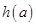 在[n,m]上的值域为[h(m),h(n)], (8分)
在[n,m]上的值域为[h(m),h(n)], (8分)∵
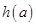 在[n,m]上的值域为[
在[n,m]上的值域为[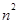 ,
,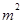 ],
],∴h(m)=n2, h(n)=m2
即:12?6m=n2 ,12?6n=m2 (9分)
两式相减得:6(m-n)=(m-n)(m+n)
又m>n>3∴m+n=6,而m>n>3时,有m+n>6,矛盾. (12分)
故满足条件的实数m,n不存在. (13分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 .
. ),f(
),f( )是否成等比数列,并证明f(
)是否成等比数列,并证明f( 为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围.
为a、b的调和平均数,记为H.若H≤f(x)≤G,求x的取值范围. 到实数集
到实数集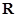 上的对应过程:区间
上的对应过程:区间 与数轴上的线段
与数轴上的线段 (不包括端点)上的点
(不包括端点)上的点 一一对应(图一),将线段
一一对应(图一),将线段 恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在
恰好重合(图二),再将这个圆放在平面直角坐标系中,使其圆心在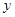 轴上,点
轴上,点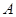 的坐标为
的坐标为 (图三).图三中直线
(图三).图三中直线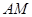 与
与 轴交于点
轴交于点 ,由此得到一个函数
,由此得到一个函数 ,则下列命题中正确的序号是 ( )
,则下列命题中正确的序号是 ( ) ;
; 是偶函数;
是偶函数; 在其定义域上是增函数;
在其定义域上是增函数;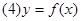 的图像关于点
的图像关于点 对称.
对称.
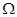 为平面直角坐标系
为平面直角坐标系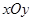 中的点集,从
中的点集,从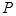 作
作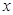 轴、
轴、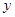 轴的垂线,垂足分别为
轴的垂线,垂足分别为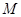 ,
,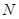 ,记点
,记点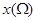 ,点
,点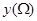 . 若
. 若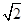 ;
;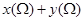 的取值范围是
的取值范围是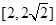 ;
;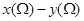 恒等于0.其中所有正确结论的序号是( )
恒等于0.其中所有正确结论的序号是( )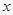 (单位:cm)满足关系:
(单位:cm)满足关系: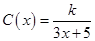 (
(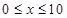 ,
,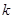 为常数),若不建隔热层,每年能源消耗费用为8万元.设
为常数),若不建隔热层,每年能源消耗费用为8万元.设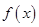 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和. 其中0
其中0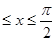
 上恒成立?
上恒成立?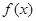 的定义域为R,若存在常数M>0,使
的定义域为R,若存在常数M>0,使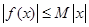 对一切实数x均成 立,则称
对一切实数x均成 立,则称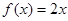 :②
:②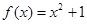 :③
:③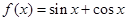 ;④
;④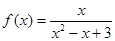 ⑤
⑤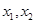 均有
均有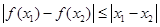 ,其中是“倍约束函数”的有( )
,其中是“倍约束函数”的有( )