题目内容
以双曲线的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为120°，则双曲线的离心率为
- A.
- B.
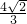
- C.
- D.
D
分析：先根据双曲线对称性可推断出四边形为菱形利用一个内角为120°推断出
=
，进而利用a，b和c关系求得a和c的关系式，即双曲线的离心率．
解答：根据双曲线对称性可推断出四边形为菱形，
∵内角为120°，∴=
平方得：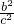
=
又∵c2=a2+b2，
所以1-
=
求得
=，
故选D
点评：本题主要考查了双曲线的简单性质．涉及求双曲线的离心率问题，解题的关键是找到a，b和c的关系．
分析：先根据双曲线对称性可推断出四边形为菱形利用一个内角为120°推断出
=，进而利用a，b和c关系求得a和c的关系式，即双曲线的离心率．解答：根据双曲线对称性可推断出四边形为菱形，
∵内角为120°，∴
=平方得：
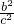=又∵c2=a2+b2，
所以1-
=求得
=，故选D
点评：本题主要考查了双曲线的简单性质．涉及求双曲线的离心率问题，解题的关键是找到a，b和c的关系．
练习册系列答案
相关题目
以双曲线的两个焦点及虚轴的两个端点为顶点的四边形中，有一个内角为120°，则双曲线的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
），则双曲线离心率的范围是 ．
