题目内容
已知以双曲线的两个焦点及虚轴的两个端点为顶点的四边形中,有一个内角的范围是(
,
),则双曲线离心率的范围是
| π |
| 3 |
| π |
| 2 |
e>
| ||
| 2 |
e>
.
| ||
| 2 |
分析:根据双曲线对称性可推断出四边形为菱形,利用有一个内角的范围是(
,
),可得
<
<1,由此可得双曲线离心率的范围.
| π |
| 3 |
| π |
| 2 |
| ||
| 3 |
| b |
| c |
解答:解:根据双曲线对称性可推断出四边形为菱形,
∵有一个内角的范围是(
,
),∴
<
<1
∴平方得:
<(
)2<1
又∵c2=a2+b2,
∴
<1-
<1
∴e>
,
故答案为:e>
.
∵有一个内角的范围是(
| π |
| 3 |
| π |
| 2 |
| ||
| 3 |
| b |
| c |
∴平方得:
| 1 |
| 3 |
| b |
| c |
又∵c2=a2+b2,
∴
| 1 |
| 3 |
| a2 |
| c2 |
∴e>
| ||
| 2 |
故答案为:e>
| ||
| 2 |
点评:本题主要考查了双曲线的简单性质,考查双曲线的离心率的范围问题,解题的关键是找到a,b和c的关系.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
 是双曲线
是双曲线 的两个焦点,点
的两个焦点,点 在双曲线上,且满足
在双曲线上,且满足 ,
则
,
则 .
.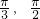 ),则双曲线离心率的范围是________.
),则双曲线离心率的范围是________. ),则双曲线离心率的范围是 .
),则双曲线离心率的范围是 .