题目内容
已知 与直线l:4x+3y-5=0切于点A的横坐标为2,
与直线l:4x+3y-5=0切于点A的横坐标为2, .
.
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调区间;
(3)若对于一切x∈[2,5],总存在x1∈[m,n],使f(x)=g(x1)成立,求n-m的最小值.
解:(1)由题意,f(2)=-1,f′(2)=-
∵ ,
,
∴
∴ ,
,
解得a=-3,b=-1,
∴
(2)∵ ,∴
,∴ ,x≠
,x≠
令 0,可得0<x<
0,可得0<x< ,或
,或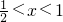 ;令f′(x)<0,可得x<0或x>1;
;令f′(x)<0,可得x<0或x>1;
∴函数的递增区间为(0, ),(
),( ,1),单调递减区间为(-∞,0),(1,+∞)
,1),单调递减区间为(-∞,0),(1,+∞)
(3)对于一切x∈[2,5],函数f(x)单调递减,所以
 ,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
∴
∴
当 时,n-m的最小值为
时,n-m的最小值为 .
.
分析:(1)求出导函数,利用f(2)=-1,f′(2)=- ,即可求函数f(x)的解析式;
,即可求函数f(x)的解析式;
(2)求导函数,令 0,可得函数的递增区间;令f′(x)<0,可得单调递减区间;
0,可得函数的递增区间;令f′(x)<0,可得单调递减区间;
(3)对于一切x∈[2,5],函数f(x)单调递减,可得 ,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则 ,由此可求n-m的最小值.
,由此可求n-m的最小值.
点评:本题考查导数知识的运用,考查函数的单调性,考查存在性问题,正确求导,确定函数的单调性是关键.

∵
 ,
,∴

∴
 ,
,
解得a=-3,b=-1,
∴

(2)∵
 ,∴
,∴ ,x≠
,x≠
令
 0,可得0<x<
0,可得0<x< ,或
,或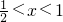 ;令f′(x)<0,可得x<0或x>1;
;令f′(x)<0,可得x<0或x>1;∴函数的递增区间为(0,
 ),(
),( ,1),单调递减区间为(-∞,0),(1,+∞)
,1),单调递减区间为(-∞,0),(1,+∞)(3)对于一切x∈[2,5],函数f(x)单调递减,所以

 ,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
∴

∴

当
 时,n-m的最小值为
时,n-m的最小值为 .
.分析:(1)求出导函数,利用f(2)=-1,f′(2)=-
 ,即可求函数f(x)的解析式;
,即可求函数f(x)的解析式;(2)求导函数,令
 0,可得函数的递增区间;令f′(x)<0,可得单调递减区间;
0,可得函数的递增区间;令f′(x)<0,可得单调递减区间;(3)对于一切x∈[2,5],函数f(x)单调递减,可得
 ,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则
,要使总存在x1∈[m,n],使f(x)=g(x1)成立,则 ,由此可求n-m的最小值.
,由此可求n-m的最小值.点评:本题考查导数知识的运用,考查函数的单调性,考查存在性问题,正确求导,确定函数的单调性是关键.

练习册系列答案
相关题目
 与直线l:4x+3y-5=0切于点A的横坐标为2,
与直线l:4x+3y-5=0切于点A的横坐标为2, .
.