题目内容
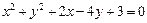
(1)若不经过坐标原点的直线
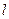 与圆C相切,且直线
与圆C相切,且直线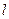 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线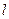 的方程;
的方程;(2)设点P在圆C上,求点P到直线
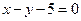 距离的最大值与最小值
距离的最大值与最小值(1)
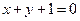 或
或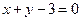
(2)最大值与最小值依次分别为
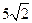 和
和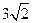
(1)圆C的方程可化为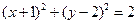 ,
,
即圆心的坐标为(-1,2),半径为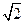 ……3分;
……3分;
因为直线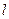 在两坐标轴上的截距相等且不经过坐标原点,
在两坐标轴上的截距相等且不经过坐标原点,
所以可设直线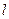 的方程为
的方程为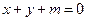 ,……1分;于是有
,……1分;于是有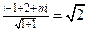 ,
,
得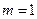 或
或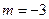 ,因此直线
,因此直线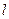 的方程为
的方程为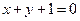 或
或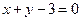 ……2分
……2分
(2)因为圆心(-1,2)到直线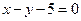 的距离为
的距离为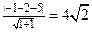 ,
,
所以点P到直线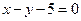 距离的最大值与最小值依次分别为
距离的最大值与最小值依次分别为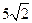 和
和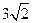 ……2分
……2分
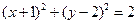 ,
,即圆心的坐标为(-1,2),半径为
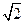 ……3分;
……3分; 因为直线
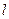 在两坐标轴上的截距相等且不经过坐标原点,
在两坐标轴上的截距相等且不经过坐标原点,所以可设直线
 的方程为
的方程为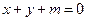 ,……1分;于是有
,……1分;于是有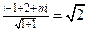 ,
,得
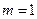 或
或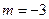 ,因此直线
,因此直线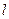 的方程为
的方程为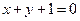 或
或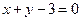 ……2分
……2分(2)因为圆心(-1,2)到直线
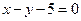 的距离为
的距离为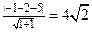 ,
,所以点P到直线
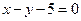 距离的最大值与最小值依次分别为
距离的最大值与最小值依次分别为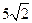 和
和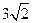 ……2分
……2分
练习册系列答案
相关题目
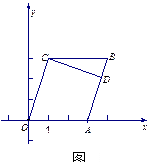
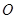 是
是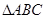 的外接圆,过点C的切线交
的外接圆,过点C的切线交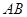 的延长线于点
的延长线于点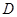 ,
,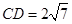 ,
,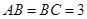 .则
.则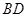 的长为 ;
的长为 ;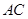 的长为 .
的长为 .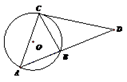
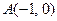 的动直线
的动直线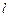 与圆
与圆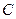 :
: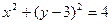 相交于
相交于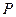 、
、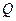 两点,
两点,  与
与 :
: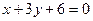 相交于
相交于 .
. 时,求直线
时,求直线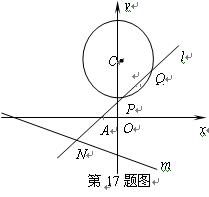
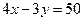 与圆
与圆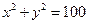 的位置关系.如果相交,求出交点坐标.
的位置关系.如果相交,求出交点坐标.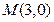 是圆
是圆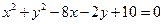 内一点,过
内一点,过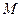 点最长的弦所在的直线的
点最长的弦所在的直线的


