题目内容
(20)设函数(Ⅰ)解不等式![]() ≤1;
≤1;
(Ⅱ)证明:当![]() ≥1时,函数
≥1时,函数![]() 在区间[0,+∞)上是单调函数。
在区间[0,+∞)上是单调函数。
(20)本小题主要考查不等式的解法、函数的单调性等基本知识,分类讨论的数学思想方法和运算、推理能力。
(Ⅰ)解:不等式![]() 即
即![]() ,
,
由此得![]() ,即
,即![]() ,其中常数
,其中常数![]() 。
。
所以,原不等式等价于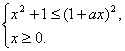
即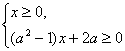
所以,当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() ;
;
当![]() 时,所给不等式的解集为
时,所给不等式的解集为![]() 。
。
(Ⅱ)证明:在区间![]() 上任取
上任取![]() 使得
使得![]()
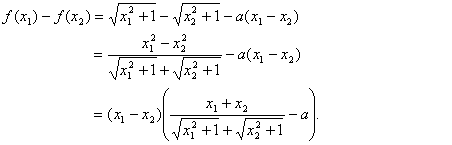
∵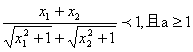 ,
,
∴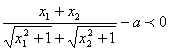 ,
,
又![]() ,
,
∴![]() ,
,
即![]() 。
。
所以,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是单调递减函数。
上是单调递减函数。

练习册系列答案
相关题目
 设函数f(x)=(a
设函数f(x)=(a| x |
| 1 | ||
|
| ∫ | 2π π |
A、-
| ||
| B、-160 | ||
| C、160 | ||
| D、20 |
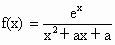 ,其中a为实数.
,其中a为实数.
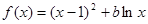 ,其中
,其中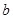 为常数.
为常数. 时,判断函数
时,判断函数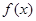 在定义域上的单调性;
在定义域上的单调性;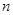 ,不等式
,不等式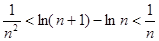 都成立.
都成立.