题目内容
(本小题满分14分)20. (14分)设函数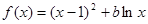 ,其中
,其中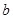 为常数.
为常数.
(1)当 时,判断函数
时,判断函数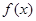 在定义域上的单调性;
在定义域上的单调性;
(2)若函数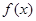 的有极值点,求
的有极值点,求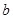 的取值范围及
的取值范围及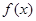 的极值点;
的极值点;
(3)求证对任意不小于3的正整数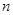 ,不等式
,不等式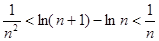 都成立.
都成立.
【答案】
(1)函数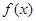 在定义域
在定义域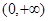 上单调递增;
上单调递增;
(2)当且仅当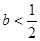 时
时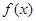 有极值点;
有极值点;
当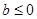 时,
时,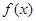 有惟一最小值点
有惟一最小值点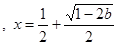 ;
;
当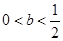 时,
时,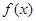 有一个极大值点
有一个极大值点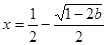 和一个极小值点
和一个极小值点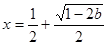 。
。
(3)证明略
【解析】(1)由题意知,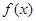 的定义域为
的定义域为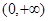 ,
,
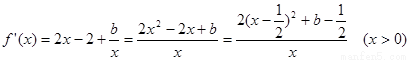 …… 1分
…… 1分
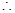 当
当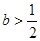 时,
时, 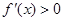 ,函数
,函数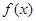 在定义域
在定义域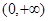 上单调递增. …… 2分
上单调递增. …… 2分
(2)设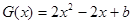 ,若函数
,若函数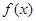 的有极值点,则G(x)
的有极值点,则G(x) =0有解
=0有解
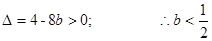 …………………3分
…………………3分
当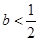 时,
时,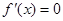 有两个不同解,
有两个不同解,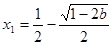
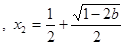
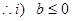 时,
时,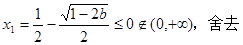 ,
,
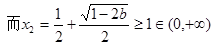 ,
,
此时 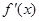 ,
,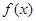 随
随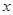 在定义域上的变化情况如下表:
在定义域上的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
减 |
极小值 |
增 |
由此表可知: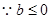 时,
时,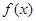 有惟一极小值点
有惟一极小值点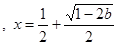 ,
,
ii) 当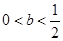 时,0<
时,0<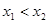 <1
此时,
<1
此时,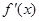 ,
,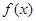 随
随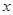 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
增 |
极大值 |
减 |
极小值 |
增 |
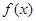 有极大值
有极大值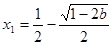 和极小值点
和极小值点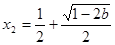 ;
;
综上所述:
当且仅当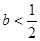 时
时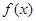 有极值点;
有极值点;
当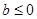 时,
时,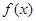 有惟一最小值点
有惟一最小值点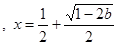 ;
;
当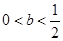 时,
时,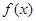 有一个极大值点
有一个极大值点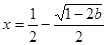 和一个极小值点
和一个极小值点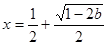
(3)由(2)可知当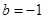 时,函数
时,函数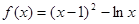 ,
,
此时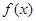 有惟一极小值点
有惟一极小值点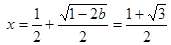
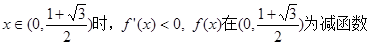
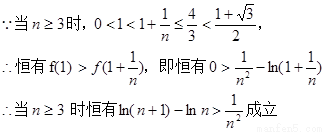
令函数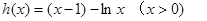
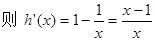
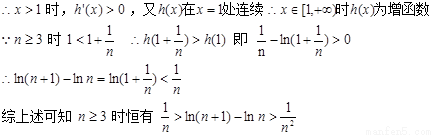

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
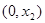
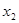
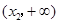

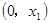
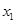
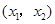
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)