题目内容
6.已知x2+y2=4,x>0,y>0,且loga(2+x)=m,loga$\frac{1}{2-x}$=n,则logay等于( )| A. | m+n | B. | m-n | C. | $\frac{1}{2}$(m+n) | D. | $\frac{1}{2}$(m-n) |
分析 化简可得loga(2-x)=-n,从而化简可得m-n=2logay,从而解得.
解答 解:∵loga$\frac{1}{2-x}$=n,∴loga(2-x)=-n,
∴m-n=loga(2+x)+loga(2-x)
=loga(4-x2)=logay2=2logay,
故logay=$\frac{m-n}{2}$;
故选:D.
点评 本题考查了对数运算性质的应用.

练习册系列答案
相关题目
16.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | $\frac{1}{3}$+π | B. | $\frac{2}{3}$+2π | C. | $\frac{8}{3}$+8π | D. | $\frac{4}{3}$+4π |
1.下列各函数中,为指数函数的是 ( )
| A. | y=3•2x | B. | y=x-2 | C. | y=πx | D. | y=(-3)x |
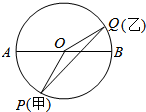 如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.
如图,有一个半径为20m的圆形水池,甲、乙两人分别从水池一条直径AB的两端开始,同时按逆时针方向绕水池边缘做匀速圆周运动,已知乙绕水池2圈需要1min,甲的速度是乙的两倍.如果从两人出发时开始计时,求当乙绕水池1周的过程中,两人的直线距离l(m)和时间t(s)的函数关系式.