题目内容
已知F1,F2为双曲线C: 的左右焦点,点P在C上,
的左右焦点,点P在C上, ,则
,则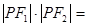 ( )
( )
| A. 2 | B. 4 | C. 6 | D. 8 |
B
解析试题分析:不妨设P在双曲线的右支上,所以 ,又因为
,又因为 ,所以在
,所以在 中利用余弦定理可知:
中利用余弦定理可知:
考点:本小题主要考查双曲线的性质,余弦定理.
点评:本小题虽然求 ,但是并没有分别求出
,但是并没有分别求出 ,这种方法要仔细掌握.
,这种方法要仔细掌握.

练习册系列答案
相关题目
从抛物线 上任意一点
上任意一点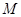 向圆
向圆 作切线
作切线 ,则切线长
,则切线长 的最小值为
的最小值为
A.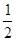 | B.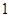 | C. | D.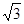 |
两圆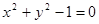 和
和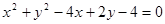 的位置关系是
的位置关系是
| A.内切 | B.相交 | C.外切 | D.外离 |
双曲线
 的两个焦点为
的两个焦点为 、
、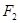 ,双曲线上一点
,双曲线上一点 到
到 的距离为12,则
的距离为12,则 到
到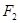 的距离为( )
的距离为( )
| A.17 | B.22 | C.7或17 | D.2或22 |
过椭圆 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )
A. | B. | C. | D. |
抛物线 的准线方程是 ( )
的准线方程是 ( )
A. | B. | C. | D. |

 与抛物线
与抛物线 相交于
相交于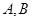 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若 ,则k的值为( )。
,则k的值为( )。



 为一个焦点的椭圆,近地点A距地面为
为一个焦点的椭圆,近地点A距地面为 千米,远地点B距地面为
千米,远地点B距地面为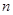 千米,地球半径为
千米,地球半径为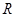 千米,则飞船运行轨道的短轴长为( )
千米,则飞船运行轨道的短轴长为( )
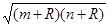

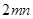
 的焦点为F,准线为l,点P为抛物线上一点,且
的焦点为F,准线为l,点P为抛物线上一点,且 ,垂足为A,若直线AF的斜率为
,垂足为A,若直线AF的斜率为 ,则|PF|等于( )
,则|PF|等于( )
