题目内容
空间四边形ABCD的对角线AC=10,BD=6,M、N分别为AB、CD的中点, MN=7,求异面直线AC和BD所成的角.
解析:如图所示,取AD的中点P,
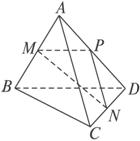
∵M、N分别为AB、CD中点,
∴PM∥BD,PN∥AC.
∴异面直线AC和BD所成的角α为∠MPN(或它的补角).
∵AC=10,BD=6,MN=7,
∴PN=![]() AC=5,PM=
AC=5,PM=![]() BD=3.
BD=3.
在△PMN中,由余弦定理知
cos∠MPN=![]() .
.
则cosα=![]() ,α∈(0,
,α∈(0,![]() ],α=60°.
],α=60°.
故AC和BD所成的角为60°.
小结:求两条异面直线所成的角的一般步骤是:
(1)构造:根据异面直线定义,用平移法作出异面直线所成的角;
(2)认定:证明作出的角就是要求的角;
(3)计算:求角值,常利用三角形;
(4)结论.

练习册系列答案
相关题目
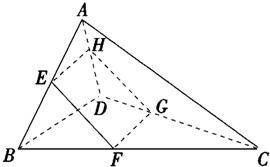 空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是
空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是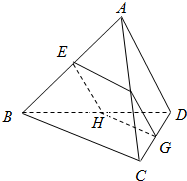 空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.
空间四边形ABCD的对棱AD,BC成60°的角,且AD=BC=a,平行于AD与BC的截面分别交AB,AC,CD,BD于E、F、G、H.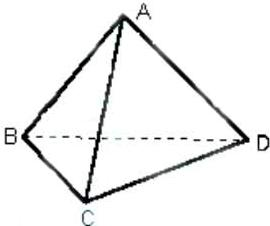 如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.
如图,一空间四边形ABCD的对边AB与CD,AD与BC都互相垂直,用向量证明:AC与BD也互相垂直.