题目内容
如图一,平行四边形ABCD关于直线AC对称,∠A=60°,∠C=90°,CD=2,把△ABD沿BD折起(如图二),使二面角A-BD-C的余弦值等于 ,对于图二,
,对于图二,
(Ⅰ)求AC;
(Ⅱ)证明:AC⊥平面BCD;
(Ⅲ)求直线AC与平面ABD所成角的正弦值。
 ,对于图二,
,对于图二,(Ⅰ)求AC;
(Ⅱ)证明:AC⊥平面BCD;
(Ⅲ)求直线AC与平面ABD所成角的正弦值。

解:(Ⅰ)取BD的中点E,连接AE,CE,
由AB=CD,CB=CD,得,AE⊥BD,CE⊥BD
∴∠AEC就是二面角A-BD-C的平面角,∴cos∠AEC=
在△ACE中,AE= ,CE=
,CE= ,
,
= ,∴AC=2
,∴AC=2
(Ⅱ)由
∴ ,
, ,∴
,∴
∴ ,又BC∩CD=C,∴AC⊥平面BCD;
,又BC∩CD=C,∴AC⊥平面BCD;
(Ⅲ)方法一:由(Ⅰ)知BD⊥平面ACE,BD 平面ABD,
平面ABD,
∴平面ACE⊥平面ABD,平面ACE∩平面ABD=AE
作CF⊥AE于F,则CF⊥平面ABD
∠CAF就是AC与平面ABD所成的角,∴sin∠CAF=sin∠CAE= ;
;
方法二:设点C到平面ABD的距离为h,
∵ ,∴
,∴
∴h= ,于是AC与平面ABD所成角
,于是AC与平面ABD所成角 的正弦为sin
的正弦为sin =
= ;
;
方法三:以CB,CD,CA所在直线分别为x轴,y轴和z轴建立的空间直角坐标轴系C-xyz,
则A(0,0,2),B(2,0,0),C(0,0,0),D(0,2,0)
设平面ABD的法向量为 =(x,y,z),则
=(x,y,z),则 ·
· =0,
=0, ·
· =0
=0 2x-2z=0,y-2z=0
2x-2z=0,y-2z=0
取 x=y=1,则 =(1,1,1),于是AC与平面ABD所成角
=(1,1,1),于是AC与平面ABD所成角 的正弦即:
的正弦即:

由AB=CD,CB=CD,得,AE⊥BD,CE⊥BD
∴∠AEC就是二面角A-BD-C的平面角,∴cos∠AEC=

在△ACE中,AE=
 ,CE=
,CE= ,
,
=
 ,∴AC=2
,∴AC=2(Ⅱ)由

∴
 ,
, ,∴
,∴
∴
 ,又BC∩CD=C,∴AC⊥平面BCD;
,又BC∩CD=C,∴AC⊥平面BCD;(Ⅲ)方法一:由(Ⅰ)知BD⊥平面ACE,BD
 平面ABD,
平面ABD,∴平面ACE⊥平面ABD,平面ACE∩平面ABD=AE
作CF⊥AE于F,则CF⊥平面ABD
∠CAF就是AC与平面ABD所成的角,∴sin∠CAF=sin∠CAE=
 ;
;方法二:设点C到平面ABD的距离为h,
∵
 ,∴
,∴
∴h=
 ,于是AC与平面ABD所成角
,于是AC与平面ABD所成角 的正弦为sin
的正弦为sin =
= ;
;方法三:以CB,CD,CA所在直线分别为x轴,y轴和z轴建立的空间直角坐标轴系C-xyz,
则A(0,0,2),B(2,0,0),C(0,0,0),D(0,2,0)
设平面ABD的法向量为
 =(x,y,z),则
=(x,y,z),则 ·
· =0,
=0, ·
· =0
=0 2x-2z=0,y-2z=0
2x-2z=0,y-2z=0取 x=y=1,则
 =(1,1,1),于是AC与平面ABD所成角
=(1,1,1),于是AC与平面ABD所成角 的正弦即:
的正弦即:

练习册系列答案
相关题目
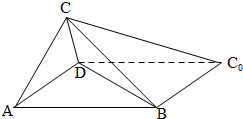 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,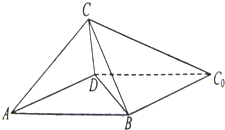 如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,
如图,一张平行四边形的硬纸片ABC0D中,AD=BD=1,