题目内容
双曲线的中心在坐标原点O,A、C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F是双曲线的左焦点,直线AB与FC相交于点D,若双曲线的离心率为2,则∠BDF的余弦值是( )
(A)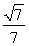 (B)
(B)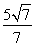 (C)
(C)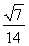 (D)
(D)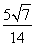
【答案】
C
【解析】设双曲线方程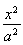 -
-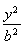 =1(a>0,b>0),
=1(a>0,b>0),
则A(0,b),C(0,-b),B(-a,0),F(-c,0),
由e=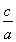 =2得c=2a,b=
=2得c=2a,b=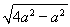 =
=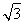 a,
a,
∴直线AB方程为y=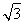 x+
x+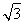 a,
a,
直线FC方程为y=-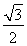 x-
x-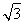 a.
a.
法一 由 得D(-
得D(-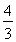 a,-
a,-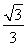 a).
a).
∴|DF|=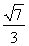 a,|DB|=
a,|DB|=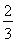 a,
a,
又|BF|=a.
在△BDF中,由余弦定理得
cos∠BDF= =
=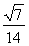 .
.
故选C.
法二 tan∠FBD=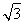 ,tan∠DFB=
,tan∠DFB=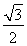 ,
,
∴tan∠BDF=tan[180°-(∠FBD+∠DFB)]
=-tan(∠FBD+∠DFB)
=-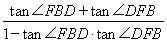
=3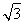 .
.
∴cos∠BDF=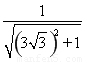 =
=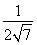 =
=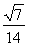 .故选C.
.故选C.

练习册系列答案
相关题目
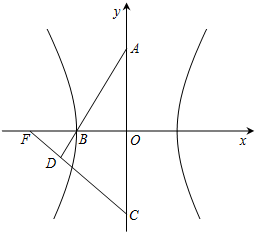 如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )
如图,双曲线的中心在坐标原点O,A,C分别是双曲线虚轴的上、下顶点,B是双曲线的左顶点,F为双曲线的左焦点,直线AB与FC相交于点D.若双曲线的离心率为2,则∠BDF的余弦值是( )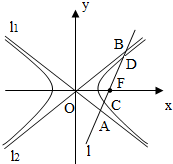 如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率
如图,双曲线的中心在坐标原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.又已知该双曲线的离心率