题目内容
【题目】已知函数
， 
， 
.
（1）设函数
，若
在区间
上单调，求实数
的取值范围；
（2）求证： 
.
【答案】（1）
的取值范围为
（2）证明见解析
【解析】试题分析：（1）求出函数的导数，问题转化为
在
上恒成立，求出m的范围即可；（2）设g(x)=f2(x)-f3(x)-2f1′(x)=ex-lnx-2，求出函数的导数，得到函数的单调性，求出g（x）的最小值，从而证出结论．
试题解析:（1）由题意得
，所以
，因为
，
所以
若函数
在区间
上单调递增，则
在
上恒成立，即
在
上恒成立，所以
若函数
在区间
上单调递减，则
在
上恒成立，
即
在
上恒成立，所以
综上，实数
的取值范围为
.
（2）设
则
，设
，则
，所以
在
上单调递增，
由
， 
得，存在唯一的
使得
，
所以在
上有
，在
上有
所以
在
上单调递减，在
递增.
所以
，故
， 
.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】某学校为倡导全体学生为特困学生捐款，举行“一元钱，一片心，诚信用水”活动，学生在购水处每领取一瓶矿泉水，便自觉向捐款箱中至少投入一元钱．现统计了连续5天的售出和收益情况，如表：
售出水量x（单位：箱） | 7 | 6 | 6 | 5 | 6 |
收益y（单位：元） | 165 | 142 | 148 | 125 | 150 |
（1）求y关于x的线性回归方程；
（2）预测售出8箱水的收益是多少元？
附：回归直线的斜率和截距的最小二乘法估计公式分别为： 
= 
， 
= 
﹣ 
，
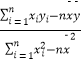参考数据：7×165+6×142+6×148+5×125+6×150=4420．
【题目】某化工厂生产甲、乙两种混合肥料，需要A，B，C三种主要原料，生产1扯皮甲种肥料和生产1车皮乙种肥料所需三种原料的吨数如表所示：
| A | B | C |
甲 | 4 | 8 | 3 |
乙 | 5 | 5 | 10 |
现有A种原料200吨，B种原料360吨，C种原料300吨，在此基础上生产甲、乙两种肥料．已知生产1车皮甲种肥料，产生的利润为2万元；生产1车品乙种肥料，产生的利润为3万元、分别用x，y表示计划生产甲、乙两种肥料的车皮数．
（1）用x，y列出满足生产条件的数学关系式，并画出相应的平面区域；
（2）问分别生产甲、乙两种肥料，求出此最大利润．