Question

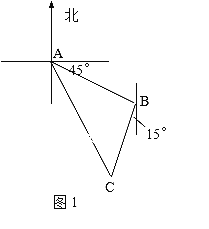
【题目】如图1，甲船在A处，乙船在A处的南偏东45°方向，距A有9n mile并以20n mile/h的速度沿南偏西15°方向航行，若甲船以28n mile/h的速度航行，应沿什么方向，用多少h能尽快追上乙船？

Answer 1

【答案】甲船沿南偏东sin的方向用h可以追上乙船。

【解析】试题分析：设th甲舰可追上乙舰，相遇点记为C

则在△ABC中，AC＝28t，BC＝20t，AB＝9，∠ABC＝120°

由余弦定理

AC2＝AB2＋BC2－2AB·BCcosABC

(28t)2＝81＋(20t)2－2×9×20t×(－)

整理得128t2－60t－27＝0

解得t＝ (t＝－舍去)

故BC＝15（nmile），AC＝21( nmile)

由正弦定理

∴sinBAC＝×＝

∠BAC＝arcsin

故甲舰沿南偏东－arcsin 的方向用0.75 h可追上乙舰.