题目内容
定义域为R的函数 ,若关于
,若关于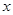 的方程
的方程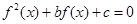 恰有5个不同的实数解
恰有5个不同的实数解 ,则
,则 ( )
( )
| A.4 | B.10 | C.12 | D.16 |
B
解析试题分析:画出函数 的图象,
的图象,
它关于x=2对称,函数值域为(0,+∞)。
因为关于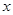 的方程
的方程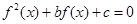 恰有5个不同的实数解
恰有5个不同的实数解 ,令
,令 ,所以关于t的方程
,所以关于t的方程 ,应有两正根,且t=1或t>0且t
,应有两正根,且t=1或t>0且t 1.
1.
所以 ,即
,即 10,故选B。
10,故选B。
考点:本题主要考查分段函数的解析式求法及其图象的作法;根的存在性及根的个数判断.
点评:画出函数 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有5个不同的整数解
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有5个不同的整数解 时,所满足的条件是解答本题的关键.
时,所满足的条件是解答本题的关键.

练习册系列答案
相关题目
若方程 无实数解,则实数
无实数解,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
给定方程: ,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
,下列命题中:(1) 该方程没有小于0的实数解;(2) 该方程有无数个实数解;(3) 该方程在(–∞,0)内有且只有一个实数解;
(4) 若x0是该方程的实数解,则x0>–1.
则正确命题的个数是 ( )
| A.1 | B.2 | C.3 | D.4 |
已知函数 ,若实数
,若实数 互不相等,且
互不相等,且 ,则
,则 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
函数f(x)= cos2x在区间[-3,3]上的零点的个数为( )
cos2x在区间[-3,3]上的零点的个数为( )
| A.3 | B.4 | C.5 | D.6 |
下列函数中是偶函数且在(0,1)上单调递减的是( )
A. | B. | C. | D. |
定义在R上的偶函数 满足:对任意的
满足:对任意的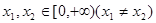 ,有
,有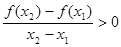 ,则( )
,则( )
A.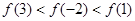 | B.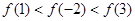 |
C.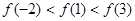 | D.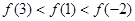 |
已知函数
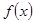 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, ,那么函数
,那么函数
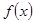 的零点个数为( )
的零点个数为( )
| A.一定是2 | B.一定是3 | C.可能是2也可能是3 | D.可能是0 |
已知函数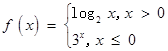 , 则
, 则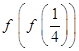 的值是
的值是
A.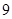 | B. | C.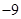 | D.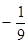 |