题目内容
如图在长方形ABCD中,AB=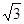 ,BC=1,E为线段DC上一动点,现将
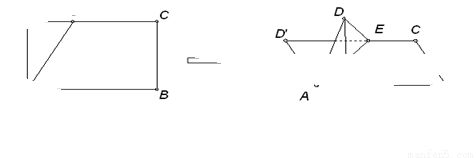
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
A.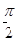 B.
B.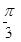 C.
C.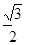 D.
D.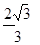
【答案】
B
【解析】
试题分析: 由题意,将
由题意,将 沿
沿 折起,使平面
折起,使平面 ⊥平面
⊥平面 ,在平面
,在平面 内过点
内过点 作
作 ,
, 为垂足,由翻折的特征知,连接
为垂足,由翻折的特征知,连接 ,则
,则 ,故
,故 点的轨迹是以
点的轨迹是以 为直径的圆上一弧,根据长方形知圆半径是
为直径的圆上一弧,根据长方形知圆半径是 ,如图当
,如图当 与
与 重合时,
重合时, ,取
,取 为
为 的中点,得到
的中点,得到 为等边三角形,故
为等边三角形,故 故所对的弧长为
故所对的弧长为
考点:本小题主要考查与二面角有关的立体几何综合题目,考查学生的空间想象能力和运算求解能力.
点评:本小题解题的关键是由题意得出点K的轨迹是圆上的一段弧,翻折问题中要注意位置关系与长度等数量的变与不变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

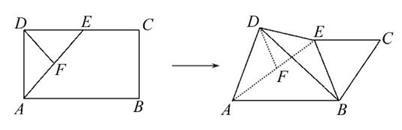
 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
( )
 B.
B.  C.
C. D.
D.
 的值.
的值.