题目内容
f(x)=|x+2|+1,g(x)=ax,对于任意的x∈R,不等式f(x)≥g(x)恒成立,则实数a的取值范围是________.
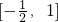
分析:利用绝对值的几何意义化简函数f(x),利用对于任意的x∈R,不等式f(x)≥g(x)恒成立,建立不等关系,即可得出结论.
解答:(1)x≥-2,f(x)=x+3,f(x)-g(x)=(1-a)x+3≥0恒成立
x=-2时,-2(1-a)+3≥0,a≥-

x>-2时,(1-a)x+3≥0,则需(1-a)非负,a≤1
所以-
 ≤a≤1;
≤a≤1;(2)x<-2,f(x)=-x-1,f(x)-g(x)=(-1-a)x-1≥0恒成立
x=-2时,-2(-1-a)-1≥0,a≥-

x<-2时,(-1-a)x-1≥0,则需(-1-a)非正,a≥-1
所以a≥-

综上,取两段的交集,-
 ≤a≤1
≤a≤1故答案为:
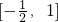
点评:本题考查恒成立问题,考查分段函数,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
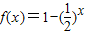 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数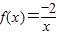 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数;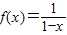 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数. 是[-1,0]上的一阶回归函数
是[-1,0]上的一阶回归函数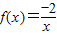 是(0,+∞)上的二阶回归函数;
是(0,+∞)上的二阶回归函数; 是(2,+∞)上的三阶回归函数.
是(2,+∞)上的三阶回归函数.