题目内容
某校在高三年级上学期期末考试数学成绩中抽取n个数学成绩进行分析,全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组[120,130],下表是按上述分组方法得到的频率分布表:
(1)求n及分布表中x,y,z的值;
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.
| 分 组 | 频 数 | 频 率 |
| [80,90) | x | 0.04 |
| [90,100) | 9 | y |
| [100,110) | z | 0.38 |
| [110,120) | 17 | 0.34 |
| [120,130] | 3 | 0.06 |
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.
(1)n=
=50t=
=50,x=50×0.04=2,y=1-0.04-0.38-0.34-0.06=0.18,z=50×0.38=19.(4分)
(2)设第5组的3名学生分别为A1,A2,A3,第1组的2名学生分别为B1,B2,则从5名学生中抽取两位学生有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共10种可能.…(6分)
第一组没有人被抽到的情况有:(A1,A2),(A1,A3),(A2,A3)三种.
所以第一组至少有一名同学被抽到的概率:1-
=
.…(8分)
(3)第1组[80,90)中有2个学生,数学测试成绩设为a,b第5组[120,130]中有3个学生,
数学测试成绩设为A,B,C,则m,n可能结果为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),
共10种,…(10分)
使|m-n|≤10成立有(a,b),(A,B),(A,C),(B,C)共4种,|m-n|>10的有6种,…(11分)
所以P(|m-n|>10)=
=
即事件“|m-n|>10”的概率为
.------(12分)
| 3 |
| 0.06 |
| 3 |
| 0.06 |
(2)设第5组的3名学生分别为A1,A2,A3,第1组的2名学生分别为B1,B2,则从5名学生中抽取两位学生有:
(A1,A2),(A1,A3),(A1,B1),(A1,B2),(A2,A3),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2),共10种可能.…(6分)
第一组没有人被抽到的情况有:(A1,A2),(A1,A3),(A2,A3)三种.
所以第一组至少有一名同学被抽到的概率:1-
| 3 |
| 10 |
| 7 |
| 10 |
(3)第1组[80,90)中有2个学生,数学测试成绩设为a,b第5组[120,130]中有3个学生,
数学测试成绩设为A,B,C,则m,n可能结果为(a,b),(a,A),(a,B),(a,C),(b,A),(b,B),(b,C),(A,B),(A,C),(B,C),
共10种,…(10分)
使|m-n|≤10成立有(a,b),(A,B),(A,C),(B,C)共4种,|m-n|>10的有6种,…(11分)
所以P(|m-n|>10)=
| 6 |
| 10 |
| 3 |
| 5 |
| 3 |
| 5 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某校从参加高三年级第一学期期末考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数,满分为100分),将数学成绩进行分组并根据各组人数制成如下频率分布表:
(Ⅰ)将上面的频率分布表补充完整,并估计本次考试全校85分以上学生的比例;
(Ⅱ)为了帮助成绩差的同学提高数学成绩,学校决定成立“二帮一”小组,即从成绩为[90,100]中任选出两位同学,共同帮助成绩在[40,50)中的某一个同学,试列出所有基本事件;若A1同学成绩为43分,B1同学成绩为95分,求A1、B1两同学恰好被安排在“二帮一”中同一小组的概率.
| 分 组 | 频 数 | 频 率 |
| [40,50 ) | 2 | 0.04 |
| [50,60 ) | 3 | 0.06 |
| [60,70 ) | 14 | 0.28 |
| [70,80 ) | 15 | 0.30 |
| [80,90 ) | ||
| [90,100] | 4 | 0.08 |
| 合 计 |
(Ⅱ)为了帮助成绩差的同学提高数学成绩,学校决定成立“二帮一”小组,即从成绩为[90,100]中任选出两位同学,共同帮助成绩在[40,50)中的某一个同学,试列出所有基本事件;若A1同学成绩为43分,B1同学成绩为95分,求A1、B1两同学恰好被安排在“二帮一”中同一小组的概率.
某校从参加高三年级第一学期期末考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数,满分为100分),将数学成绩进行分组并根据各组人数制成如下频率分布表:
(Ⅰ)将上面的频率分布表补充完整,并估计本次考试全校85分以上学生的比例;
(Ⅱ)为了帮助成绩差的同学提高数学成绩,学校决定成立“二帮一”小组,即从成绩为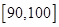 中任出两位同学,共同帮助成绩在
中任出两位同学,共同帮助成绩在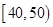 中的某一个同学,试列出所有基本事件;若
中的某一个同学,试列出所有基本事件;若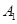 同学成绩为43分,
同学成绩为43分,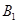 同学成绩为95分,求
同学成绩为95分,求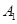 、
、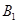 两同学恰好被安排在“二帮一”中同一小组的概率.
两同学恰好被安排在“二帮一”中同一小组的概率.
|
分 组[来源:Zxxk.Com] |
频 数 |
频 率 |
|
[ 40, 50 ) |
2 |
0.04 |
|
[ 50, 60 ) |
3 |
0.06 |
|
[60, 70 ) |
14 |
0.28 |
|
[ 70, 80 ) |
15 |
0.30 |
|
[ 80, 90 ) |
|
|
|
[ 90, 100 ] |
4 |
0.08 |
|
合 计 |
|
|
某校在高三年级上学期期末考试数学成绩中抽取n个数学成绩进行分析,全部介于80分与130分之间,将测试结果按如下方式分成五组,第一组[80,90);第二组[90,100)…第五组[120,130],下表是按上述分组方法得到的频率分布表:
(1)求n及分布表中x,y,z的值;
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.
| 分 组 | 频 数 | 频 率 |
| [80,90) | x | 0.04 |
| [90,100) | 9 | y |
| [100,110) | z | 0.38 |
| [110,120) | 17 | 0.34 |
| [120,130] | 3 | 0.06 |
(2)校长决定从第一组和第五组的学生中随机抽取2名进行交流,求第一组至少有一人被抽到的概率.
(3)设从第一组或第五组中任意抽取的两名学生的数学测试成绩分别记为m,n,求事件“|m-n|>10”的概率.