题目内容
6.已知p:“?x∈R,x2+3x-6>0”的否定是“?x0∈R,x02+3x0-6<0”,q:“a=2”是“直线ax-2y+1=0与直线ax+2y+3=0垂直”的充分不必要条件,则下列命题中是假命题的为( )| A. | p∧q | B. | p∨q | C. | ¬p∧q | D. | ¬p∨q |
分析 p:利用命题的否定即可判断出真假;利用两条直线相互垂直的充要条件即可判断出命题q的真假.再利用复合命题真假的判定方法即可得出.
解答 解:p:“?x∈R,x2+3x-6>0”的否定是“?x0∈R,x02+3x0-6≤0”,因此是假命题.
q:a=0,直线ax-2y+1=0与直线ax+2y+3=0垂直,分别化为:2y-1=0,2y+3=0,此时两条直线不垂直,舍去.
a≠0时,∵两条直线垂直,∴$\frac{a}{2}×(-\frac{a}{2})$=-1,解得a=±2.因此:“a=2”是“直线ax-2y+1=0与直线ax+2y+3=0垂直”的充分不必要条件,是真命题.
则下列命题中是假命题的为A.
故选:A.
点评 本题考查了简易逻辑的判定方法、相互垂直的直线的充要条件,考查了分类讨论方法、推理能力与计算能力,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
14.F是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,过点F且垂直于一条渐近线的直线与另一条渐近线于点B,垂足为A,若2$\overrightarrow{FA}$+$\overrightarrow{FB}$=$\overrightarrow{0}$,则C的离心率e=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
1.已知A、B为椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1与双曲线$\frac{{x}^{2}}{4}$$-\frac{{y}^{2}}{3}$=1的公共顶点M、N分别为椭圆和双曲线上一点(异于点A、B),$\overrightarrow{AM}$$+\overrightarrow{BM}$=λ($\overrightarrow{AN}$$+\overrightarrow{BN}$)(λ∈R),设直线AM、BM、AN、BN的斜率分别为k1、k2、k3、k4,则k1+k2+k3+k4=( )
| A. | -$\frac{3}{2}$ | B. | 0 | C. | $\frac{3}{2}$ | D. | $\frac{4\sqrt{3}}{3}$ |
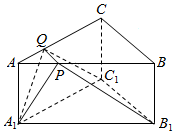 已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.
已知在直三棱柱ABC-A1B1C1中,底面是边长为2的正三角形,侧棱AA1的长为$\frac{{\sqrt{3}}}{2}$,P、Q分别是AB、AC上的点,且PQ∥BC,如图.