题目内容

【题目】某班一次数学考试成绩频率分布直方图如图所示，数据分组依次为，已知成绩大于等于分的人数为人，现采用分层抽样的方式抽取一个容量为的样本.

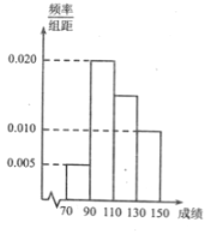
（1）求每个分组所抽取的学生人数；

（2）从数学成绩在的样本中任取人，求恰有人成绩在的概率.

【答案】（1）；（2）.

【解析】

试题分析：（1）数学成绩在内的频率分别为.比为，所以采用分层抽样的方式抽取一个容量为的样本，人数分别为；（2）由（1）可知，从两组抽取人数分别为人和人，利用列举法求得总事件有种，其中符合题意的有种，故概率为.

试题解析：

（1）由频率分布直方图可知，

数学成绩在内的频率分别为.

∴成绩在内的人数之比为，

∴采用分层抽样的方式抽取一个容量为的样本，成绩在内所抽取的人数分别为.

（2）由（1）可知，从两组抽取人数分别为人和人，

记从中抽取的人分别为，从中抽取的人分别为，从这个人中任取人，有，

共计种等可能的结果，其中恰有人成绩在包含，共计种等可能的结果，

∴抽取的人中恰有人成绩在的概率.

练习册系列答案
相关题目

【题目】在直角坐标系中，，动点满足（且）.

（1）求动点的轨迹方程，并说明轨迹是什么曲线；

（2）若，点为动点的轨迹曲线上的任意一点，过点作圆：的切线，切点为.试探究平面内是否存在定点，使为定值，若存在，请求出点的坐标，若不存在，请说明理由.

【题目】在中，内角的对边分别为，已知.

（Ⅰ）求角的值；

（Ⅱ）若，当取最小值时，求的面积.

【题目】如图，PA垂直于矩形ABCD所在的平面，E、F分别是AB、PD的中点，∠ADP＝45°.

（1）求证：AF∥平面PCE.

（2）求证：平面PCD⊥平面PCE.

（3）若AD＝2，CD＝3，求点F到平面PCE的距离．

【题目】如图，已知四棱锥P－ABCD的底面是边长为1的正方形，且侧棱PC⊥底面ABCD，且PC＝2，E是侧棱PC上的动点

（1）求四棱锥P－ABCD的体积；

（2）证明：BD⊥AE。

（3）求二面角P-BD-C的正切值。

【题目】如图，在平面直角坐标系中，已知椭圆：的离心率，左顶点为，过点作斜率为的直线交椭圆于点，交轴于点.

（1）求椭圆的方程;

（2）已知为的中点，存在定点，使得对于任意的都有，求点的坐标;

（3）若过点作直线的平行线交椭圆于点，求的最小值.

【题目】设函数．

（1）当时，设，求证：对任意的，；

（2）当时，若对任意，不等式恒成立，求实数的取值范围．

【题目】在平面直角坐标系中，已知椭圆：（）的左焦点为，且点在上.

(1)求椭圆的方程;

(2)设直线同时与椭圆和抛物线：相切，求直线的方程.

【题目】某车间甲组有10名工人，其中有4名女工人；乙组有10名工人，其中有6名女工人．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组共抽取4名工人进行技术考核．

（1）求从甲、乙两组各抽取的人数；

（2）求从甲组抽取的工人中恰有1名女工人的概率；

（3）求抽取的4名工人中恰有2名男工人的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网