题目内容
在对某校高一学生体育选修项目的一次调查中,共调查了160人,其中女生85人,男生75人.女生中有60人选修排球,其余的人选修篮球;男生中有20人选修排球,其余的人选修篮球.(每人必须选一项,且只能选一项)
根据以上数据建立一个2×2的列联表;
能否在犯错误的概率不超过0.001的前提下认为性别与体育选修项目有关?
参考公式及数据:
 ,其中
,其中 .
.| K2≥k0 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据题中数据,建立一个2×2的列联表如下:

(2)能在犯错误的概率不超过0.001的情况下认为性别与体育选修项目有关.
| | 女生 | 男生 | 合计 |
| 选排球 | 60 | 20 | 80 |
| 选篮球 | 25 | 55 | 80 |
| 合计 | 85 | 75 | 160 |

(2)能在犯错误的概率不超过0.001的情况下认为性别与体育选修项目有关.
试题分析:(1)根据题中数据,建立一个2×2的列联表如下:
| | 女生 | 男生 | 合计 |
| 选排球 | 60 | 20 | 80 |
| 选篮球 | 25 | 55 | 80 |
| 合计 | 85 | 75 | 160 |

(2)
 ,
, 
且
 ,
, ,
, 
所以能在犯错误的概率不超过0.001的情况下认为性别与体育选修项目有关.

点评:简单题,此类问题要注意理解列联表的应用,运用“卡方公式”计算并与数表比较。难度不大,公式也不要求记忆。

练习册系列答案
相关题目
 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得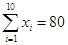 ,
, ,
, ,
, .
. 对月收入
对月收入 的线性回归方程
的线性回归方程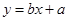 ;
; ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为
 ,
, ,
, 年多于10人的概率.
年多于10人的概率. 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出 关于
关于 的回归方程
的回归方程 ,并计算第
,并计算第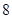 年的估计值。
年的估计值。

 次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为
次体育测试中的成绩统计如茎叶图所示,若甲、乙两人的平均成绩分别为 ,则下列结论正确的是( )
,则下列结论正确的是( )
 ;乙比甲成绩稳定
;乙比甲成绩稳定 ;甲比乙成绩稳定
;甲比乙成绩稳定
 .
.
 )
)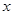 与销售额
与销售额 的统计数据如下表:
的统计数据如下表: .由此预测销售额为100万元时,投入的销售成本大约为 ;
.由此预测销售额为100万元时,投入的销售成本大约为 ; 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )