题目内容
已知椭圆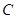 的中心在原点,一个焦点
的中心在原点,一个焦点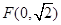 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是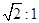 .若椭圆
.若椭圆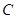 在第一象限的一点
在第一象限的一点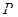 的横坐标为1,过点
的横坐标为1,过点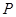 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线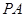 ,
,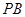 分别交椭圆
分别交椭圆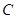 于另外两点
于另外两点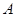 ,
,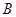 .
.
(Ⅰ)求椭圆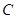 的方程;
的方程;
(Ⅱ)求证:直线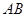 的斜率为定值;
的斜率为定值;
(Ⅲ)求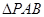 面积的最大值.
面积的最大值.
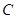 的中心在原点,一个焦点
的中心在原点,一个焦点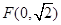 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是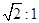 .若椭圆
.若椭圆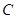 在第一象限的一点
在第一象限的一点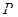 的横坐标为1,过点
的横坐标为1,过点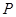 作倾斜角互补的两条不同的直线
作倾斜角互补的两条不同的直线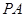 ,
,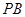 分别交椭圆
分别交椭圆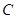 于另外两点
于另外两点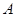 ,
,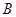 .
.(Ⅰ)求椭圆
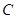 的方程;
的方程;(Ⅱ)求证:直线
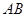 的斜率为定值;
的斜率为定值;(Ⅲ)求
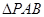 面积的最大值.
面积的最大值.(Ⅰ)设椭圆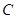 的方程为
的方程为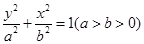 .
.

由题意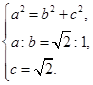 ………………………2分
………………………2分
解得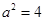 ,
,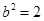 .所以椭圆
.所以椭圆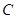 的方程为
的方程为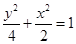 .……………4分
.……………4分
(Ⅱ)由题意知,两直线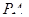 ,
,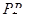 的斜率必存在,设
的斜率必存在,设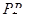 的斜率为
的斜率为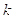 ,则
,则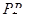 的直线方程为
的直线方程为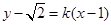 .
.
由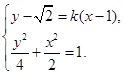 得
得
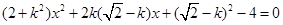 .………………6分
.………………6分
设 ,
,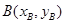 ,则
,则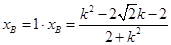 ,同理可得
,同理可得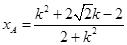 ,
,
则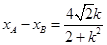 ,
,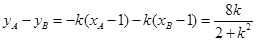 .
.
所以直线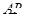 的斜率
的斜率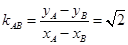 为定值. ……………………8分
为定值. ……………………8分
(Ⅲ)设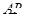 的直线方程为
的直线方程为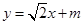 .由
.由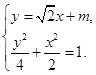 得
得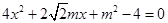 .
.
由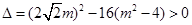 ,得
,得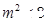 .……………………10分
.……………………10分
此时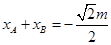 ,
,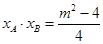 .
.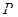 到
到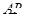 的距离为
的距离为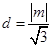 ,
,
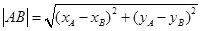
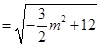 则
则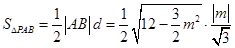
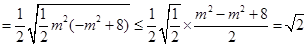 .
.
因为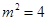 使判别式大于零,所以当且仅当
使判别式大于零,所以当且仅当 时取等号,所以
时取等号,所以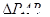 面积的最大值为
面积的最大值为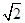 .…12分
.…12分
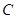 的方程为
的方程为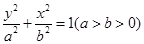 .
.
由题意
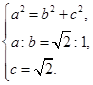 ………………………2分
………………………2分解得
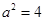 ,
,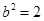 .所以椭圆
.所以椭圆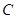 的方程为
的方程为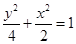 .……………4分
.……………4分(Ⅱ)由题意知,两直线
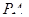 ,
,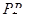 的斜率必存在,设
的斜率必存在,设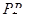 的斜率为
的斜率为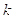 ,则
,则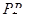 的直线方程为
的直线方程为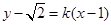 .
.由
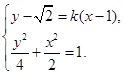 得
得 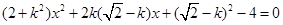 .………………6分
.………………6分设
 ,
,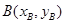 ,则
,则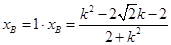 ,同理可得
,同理可得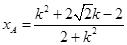 ,
, 则
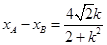 ,
,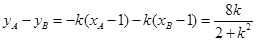 .
.所以直线
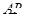 的斜率
的斜率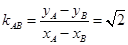 为定值. ……………………8分
为定值. ……………………8分(Ⅲ)设
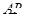 的直线方程为
的直线方程为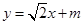 .由
.由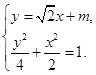 得
得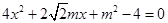 .
. 由
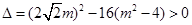 ,得
,得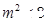 .……………………10分
.……………………10分此时
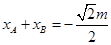 ,
,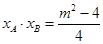 .
.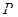 到
到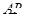 的距离为
的距离为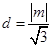 ,
,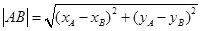
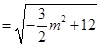 则
则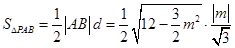
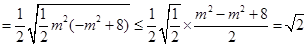 .
.因为
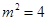 使判别式大于零,所以当且仅当
使判别式大于零,所以当且仅当 时取等号,所以
时取等号,所以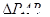 面积的最大值为
面积的最大值为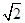 .…12分
.…12分(1)由题目条件知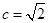 ,并且还知道
,并且还知道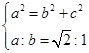 , 从而解出a,b的值.
, 从而解出a,b的值.
(2)先设直线PB的方程为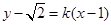 , 它与椭圆方程联立,消去y后得关于x的一元二次方程,根据1和点B的横坐标为方程的两个根,借助韦达定理,求出B的横坐标,同时可求出A的横坐标,从而求出
, 它与椭圆方程联立,消去y后得关于x的一元二次方程,根据1和点B的横坐标为方程的两个根,借助韦达定理,求出B的横坐标,同时可求出A的横坐标,从而求出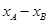 ,再借助其直接方程可求出
,再借助其直接方程可求出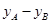 ,证明出
,证明出 为定值.
为定值.
(III) 设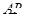 的直线方程为
的直线方程为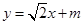 , 它与椭圆方程联立消y得关于x的一元二次方程,由弦长公式求出|AB|的长,然后再借助点到直线的距离公式求出高,从而用m表示出
, 它与椭圆方程联立消y得关于x的一元二次方程,由弦长公式求出|AB|的长,然后再借助点到直线的距离公式求出高,从而用m表示出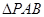 的面积.再利用函数的方法求最值即可
的面积.再利用函数的方法求最值即可
(Ⅰ)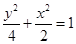 .(Ⅱ)
.(Ⅱ)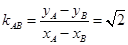 为定值.(Ⅲ)
为定值.(Ⅲ)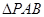 面积的最大值为
面积的最大值为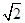
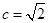 ,并且还知道
,并且还知道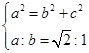 , 从而解出a,b的值.
, 从而解出a,b的值.(2)先设直线PB的方程为
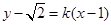 , 它与椭圆方程联立,消去y后得关于x的一元二次方程,根据1和点B的横坐标为方程的两个根,借助韦达定理,求出B的横坐标,同时可求出A的横坐标,从而求出
, 它与椭圆方程联立,消去y后得关于x的一元二次方程,根据1和点B的横坐标为方程的两个根,借助韦达定理,求出B的横坐标,同时可求出A的横坐标,从而求出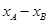 ,再借助其直接方程可求出
,再借助其直接方程可求出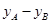 ,证明出
,证明出 为定值.
为定值.(III) 设
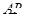 的直线方程为
的直线方程为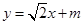 , 它与椭圆方程联立消y得关于x的一元二次方程,由弦长公式求出|AB|的长,然后再借助点到直线的距离公式求出高,从而用m表示出
, 它与椭圆方程联立消y得关于x的一元二次方程,由弦长公式求出|AB|的长,然后再借助点到直线的距离公式求出高,从而用m表示出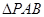 的面积.再利用函数的方法求最值即可
的面积.再利用函数的方法求最值即可(Ⅰ)
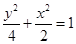 .(Ⅱ)
.(Ⅱ)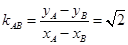 为定值.(Ⅲ)
为定值.(Ⅲ)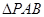 面积的最大值为
面积的最大值为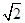

练习册系列答案
相关题目
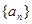 ,
, 中,
中,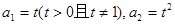 ,且
,且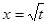 是函数
是函数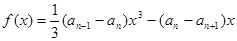 的一个极值点.
的一个极值点.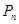 的坐标为(1,
的坐标为(1,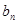 )(
)(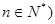 ,过函数
,过函数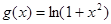 图像上的点
图像上的点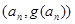 的切线始终与
的切线始终与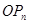 平行(O 为原点),求证:当
平行(O 为原点),求证:当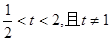 时,不等式
时,不等式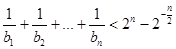 对任意
对任意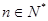 都成立.
都成立.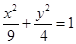 ,
,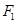 、
、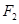 为其左右焦点,点
为其左右焦点,点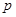 为椭圆上一点,且
为椭圆上一点,且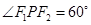 ,
,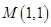 .
.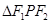 的面积. (2)直线
的面积. (2)直线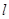 过点
过点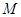 与椭圆交于
与椭圆交于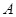 、
、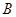 两点,若
两点,若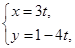 (
(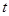 为参数)与圆
为参数)与圆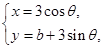 (
(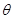 为参数)相切,则
为参数)相切,则 ( )
( )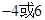
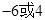
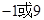
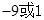
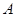 、
、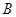 分别是直线
分别是直线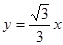 和
和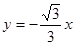 上的两个动点,线段
上的两个动点,线段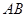 的长为
的长为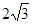 ,
,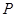 是
是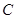 的方程;
的方程;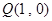 任意作直线
任意作直线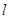 (与
(与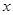 轴不垂直),设
轴不垂直),设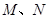 两点,与
两点,与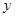 轴交于
轴交于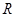 点.若
点.若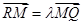 ,
,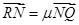 ,证明:
,证明: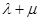 为定值.
为定值.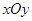 中,设点
中,设点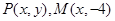 ,坐标原点
,坐标原点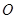 在以线段
在以线段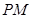 为直径的圆上
为直径的圆上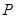 的轨迹C的方程;
的轨迹C的方程;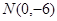 的直线
的直线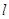 与轨迹C交于两点
与轨迹C交于两点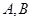 ,点
,点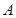 关于
关于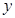 轴的对称点为
轴的对称点为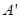 ,试判断直线
,试判断直线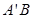 是否恒过一定点,并证明你的结论.
是否恒过一定点,并证明你的结论.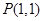 且与曲线
且与曲线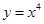 相切的切线与直线
相切的切线与直线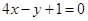 的位置关系是
的位置关系是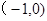 的抛物线的标准方程为( )
的抛物线的标准方程为( )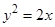
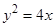
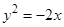
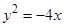
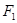 、
、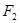 是椭圆
是椭圆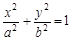
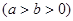 的左、右焦点,
的左、右焦点,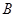 是该椭圆短轴的一个端点,直线
是该椭圆短轴的一个端点,直线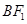 与椭圆
与椭圆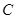 交于点
交于点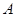 ,若
,若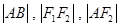 成等差数列,则该椭圆的离心率为 .
成等差数列,则该椭圆的离心率为 .