题目内容
12．求证：若奇函数f（x）存在反函数，则反函数必为奇函数．分析 根据奇函数的性质得出f-1（-x）和f-1（x）的关系，利用函数奇偶性的定义得出结论．
解答 解：设奇函数f（x）的反函数为f-1（x），∵f（x）是奇函数，∴f（x）的值域关于原点对称，即f-1（x）的定义域关于原点对称．
假设f（x）=y，则f（-x）=-y．∴f-1（y）=x，f-1（-y）=-x．
∴f-1（-y）=-f-1（y），即f-1（-x）=-f-1（x）
∴f-1（x）是奇函数．
点评 本题考查了反函数的定义，函数奇偶性的判断，属于基础题．
练习册系列答案
相关题目
20．
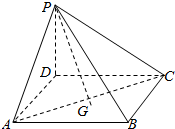如图，在四棱锥P-ABCD中，PD⊥底面ABCD，ABCD为正方形，且PD=AB=1，G为△ABC的重心，则PG与底面所成的角θ满足（ ）
如图，在四棱锥P-ABCD中，PD⊥底面ABCD，ABCD为正方形，且PD=AB=1，G为△ABC的重心，则PG与底面所成的角θ满足（ ）| A． | θ=$\frac{π}{4}$ | B． | cosθ=$\frac{2\sqrt{34}}{17}$ | C． | tanθ=$\frac{2\sqrt{2}}{3}$ | D． | sinθ=$\frac{\sqrt{3}}{3}$ |
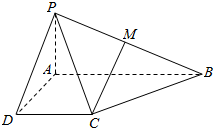如图，在四棱锥P-ABCD中，已AB∥CD，AB=2DC，M为PB的中点．