题目内容
若数列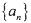 满足:
满足: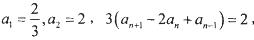
(I) 证明数列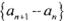 是等差数列;.
是等差数列;.
(II) 求使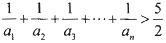 成立的最小的正整数n
成立的最小的正整数n
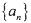 满足:
满足: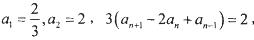
(I) 证明数列
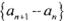 是等差数列;.
是等差数列;.(II) 求使
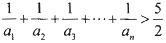 成立的最小的正整数n
成立的最小的正整数n(Ⅰ)由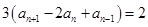 可得:
可得: 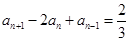 ,
,
即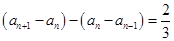 ,┄┄┄┄┄┄┄┄ 4分
,┄┄┄┄┄┄┄┄ 4分
所以数列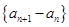 是以
是以 为首项,
为首项,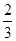 为公差的等差数列; ┄┄5分
为公差的等差数列; ┄┄5分
(Ⅱ)由(1)知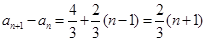 ,┄┄┄┄┄┄┄┄ 6分
,┄┄┄┄┄┄┄┄ 6分
于是累加求和得: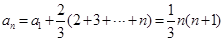 ,┄┄┄┄┄┄8分
,┄┄┄┄┄┄8分
所以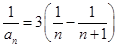 ,┄┄┄┄┄┄┄┄┄┄┄┄┄10分
,┄┄┄┄┄┄┄┄┄┄┄┄┄10分
进而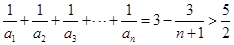
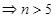 ,∴最小的正整数为
,∴最小的正整数为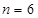
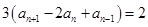 可得:
可得: 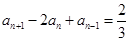 ,
,即
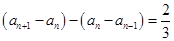 ,┄┄┄┄┄┄┄┄ 4分
,┄┄┄┄┄┄┄┄ 4分所以数列
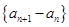 是以
是以 为首项,
为首项,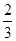 为公差的等差数列; ┄┄5分
为公差的等差数列; ┄┄5分(Ⅱ)由(1)知
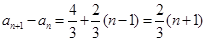 ,┄┄┄┄┄┄┄┄ 6分
,┄┄┄┄┄┄┄┄ 6分于是累加求和得:
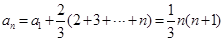 ,┄┄┄┄┄┄8分
,┄┄┄┄┄┄8分所以
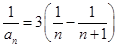 ,┄┄┄┄┄┄┄┄┄┄┄┄┄10分
,┄┄┄┄┄┄┄┄┄┄┄┄┄10分进而
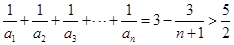
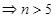 ,∴最小的正整数为
,∴最小的正整数为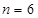
略

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
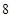
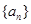 的各项均为正数,
的各项均为正数,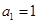 ,前
,前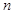 项和为
项和为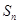 ;
;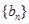 为等比数列,
为等比数列,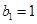 ,且
,且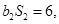
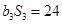 ,
,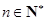 .(Ⅰ)求数列
.(Ⅰ)求数列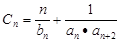 ,
,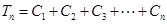 ;
;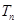 ;②当
;②当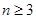 时,证明:
时,证明: .
.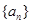 的前n项和为
的前n项和为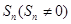 ,且
,且 ,
,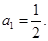
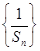 是等差数列;
是等差数列;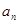 ;
;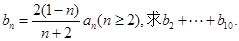
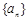 的前
的前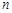 项和为
项和为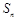 ,且
,且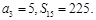
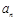 ;(Ⅱ)设
;(Ⅱ)设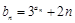 ,求数列
,求数列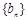 的前
的前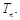
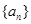 的前n项和为
的前n项和为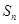 ,若
,若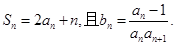
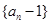 为等比数列;
为等比数列;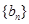 的前n项和。
的前n项和。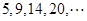 为“梯形数”.根据图形的构成,此数列的第2012项与5的差,即
为“梯形数”.根据图形的构成,此数列的第2012项与5的差,即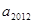 -5= ( )
-5= ( )


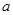 , b的等差中项是
, b的等差中项是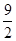 ,等比中项为2
,等比中项为2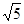 ,且
,且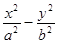 =1的离心率为 。
=1的离心率为 。