Question

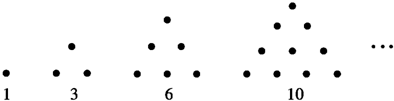
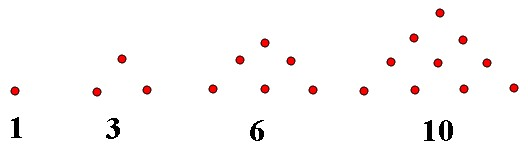
传说古希腊毕达哥拉斯学派的数学家经常在沙滩上画点或用小石子表示数．他们研究过如图所示的三角形数：将三角形数1，3，6，10，…记为数列{a_n}，将可被5整除的三角形数按从小到大的顺序组成一个新数列{b_n}．可以推测：b₂₀₁₂是数列{a_n}中的第______项．

Answer 1

由前四组可以推知a_n=

n(n+1)

2

，
从而b₁=a₄=10，b₂=a₅=15，b₃=a₉=45，b₄=a₁₀=55，
依次可知，当n=4，5，9，10，14，15，19，20，24，25，…时，
a_n能被5整除，由此可得，b_2k=a_5k（k∈N^*），
∴b₂₀₁₂=a_5×1006=a₅₀₃₀．
故答案为：5030．