题目内容
已知f(x)=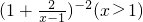 .
.
(1)求函数f(x)的反函数f-1(x)的解析式及其定义域;
(2)判断函数f-1(x)在其定义域上的单调性并加以证明;
(3)若当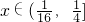 时,不等式
时,不等式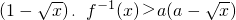 恒成立,试求a的取值范围.
恒成立,试求a的取值范围.
解:(1)令y=x,则有x=
解得: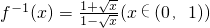 ;(4分)
;(4分)
(2)设0<x1<x2<1,则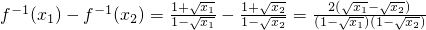
=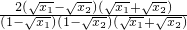 =
=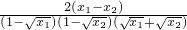
由0<x1<x2<1,有所以f-1(x1)-f-1(x2)<0,即函数f-1(x)在其定义域上的单调递增.(8分)
(3)当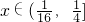 时,不等式
时,不等式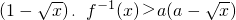 恒成立,
恒成立,
即不等式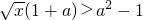 恒成立
恒成立
当1+a>0即a>-1时,原命题等价于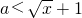 恒成立,由
恒成立,由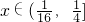
所以 ,从而得
,从而得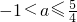
当1+a=0即a=-1时,不等式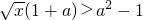 不成立
不成立
当1+a<0即a<-1时,原命题等价于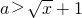 恒成立,
恒成立,
由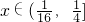 所以
所以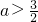 ,又a<-1,所以a不存在.综上可得:
,又a<-1,所以a不存在.综上可得: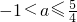 .(12分)
.(12分)
分析:(1)将x,y互换,解得y即可.
(2)用单调性定义证明,先任取两变量,界定大小,再作差变形看符号.
(3)将反函数代入,整理为不等式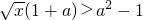 恒成立求解,注意讨论.
恒成立求解,注意讨论.
点评:本题主要考查如何求函数的反函数,单调性定义证明及不等式恒成立问题.

解得:
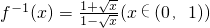 ;(4分)
;(4分)(2)设0<x1<x2<1,则
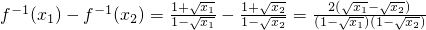
=
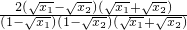 =
=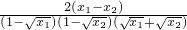
由0<x1<x2<1,有所以f-1(x1)-f-1(x2)<0,即函数f-1(x)在其定义域上的单调递增.(8分)
(3)当
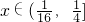 时,不等式
时,不等式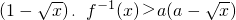 恒成立,
恒成立,即不等式
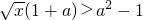 恒成立
恒成立当1+a>0即a>-1时,原命题等价于
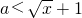 恒成立,由
恒成立,由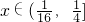
所以
 ,从而得
,从而得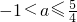
当1+a=0即a=-1时,不等式
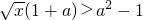 不成立
不成立当1+a<0即a<-1时,原命题等价于
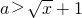 恒成立,
恒成立,由
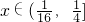 所以
所以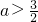 ,又a<-1,所以a不存在.综上可得:
,又a<-1,所以a不存在.综上可得: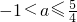 .(12分)
.(12分)分析:(1)将x,y互换,解得y即可.
(2)用单调性定义证明,先任取两变量,界定大小,再作差变形看符号.
(3)将反函数代入,整理为不等式
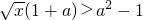 恒成立求解,注意讨论.
恒成立求解,注意讨论.点评:本题主要考查如何求函数的反函数,单调性定义证明及不等式恒成立问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目