题目内容
在△ABC中，a，b，c分别是∠A，∠B，∠C的对边，已知b2＝c(b＋2c)，若a＝
，cos A＝
，则△ABC的面积等于( )
，cos A＝，则△ABC的面积等于( )A． | B． |
C． | D．3 |
C
∵b2＝c(b＋2c)，∴b2－bc－2c2＝0，
即(b＋c)·(b－2c)＝0，∴b＝2c.
又a＝，cos A＝
＝，
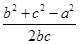解得c＝2，b＝4.
∴S△ABC＝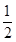
bcsin A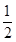＝×4×2×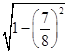
＝.
即(b＋c)·(b－2c)＝0，∴b＝2c.
又a＝
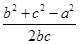，cos A＝＝，解得c＝2，b＝4.
∴S△ABC＝
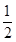bcsin A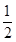＝×4×2×＝.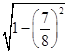
练习册系列答案
相关题目
中，角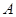
、
、
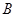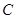所对的边长分别为
、
、
，
． 
，
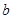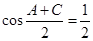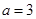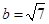，求
，求
的取值范围．
,BC=2,∠B=60°,则△ABC的面积等于 . 
.
-cos 2A的值.
,求bc的最大值.
，灯塔A在观测站Ｃ的北偏东
，灯塔Ｂ在观测站Ｃ的南偏东
,则灯塔A与灯塔Ｂ的距离为（ ）
B．
C．
Ｄ．
的焦点为
，点
在椭圆上，若
，
的小大为 ．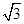
的重心为G，内角A，B，C的对边分别为a，b，c，若
，则角A为（ ）
