题目内容
【题目】已知数列{![]() }中,
}中, ![]() ,且
,且![]() 对任意正整数都成立,数列{
对任意正整数都成立,数列{![]() }的前n项和为Sn。
}的前n项和为Sn。
(1)若![]() ,且
,且![]() ,求a;
,求a;
(2)是否存在实数k,使数列{![]() }是公比不为1的等比数列,且任意相邻三项
}是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k值,若不存在,请说明理由;
(3)若![]() 。
。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
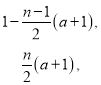
![]()
【解析】试题分析:(1)![]() 时,
时, ![]() ,由等差数列定义知数列
,由等差数列定义知数列![]() 是等差数列,由
是等差数列,由![]() 可得
可得![]() ,解得
,解得![]() ,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{
,(2)等差数列与等比数列的综合,从等差数列列等量关系:因为数列{![]() }是公比不为1,所以
}是公比不为1,所以![]() 不为等差中项,只需讨论
不为等差中项,只需讨论![]() 与
与![]() 为等差中项:若
为等差中项:若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得: ![]() ,解得
,解得![]() (舍1);
(舍1); ![]() ;同理若
;同理若![]() 为等差中项,
为等差中项, ![]() (3)
(3)![]() 则
则![]() ,
, ![]() ,从而
,从而![]() ,所以求和时要重新组合,每两项作为一组,先求
,所以求和时要重新组合,每两项作为一组,先求![]() 是偶数时,
是偶数时, ![]()
![]()
![]() ,再求
,再求![]() 是奇数时,
是奇数时, ![]()
![]()
![]()
![]()
![]() ,
,
试题解析:(1)![]() 时,
时, ![]() ,
, ![]() ,所以数列
,所以数列![]() 是等差数列 1分
是等差数列 1分
此时首项![]() ,公差
,公差![]() ,数列
,数列![]() 的前
的前![]() 项和是
项和是![]() 3分
3分
故![]() ,即
,即![]() ,得
,得![]() ; 4分
; 4分
(没有过程,直接写![]() 不给分)
不给分)
(2)设数列![]() 是等比数列,则它的公比
是等比数列,则它的公比![]() ,所以
,所以![]() ,
, ![]() ,
, ![]() 6分
6分
①若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,解得:
,解得: ![]() ,不合题意;
,不合题意;
②若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得: ![]() ,
,
解得![]() (舍1);
(舍1); ![]() ;
;
③若![]() 为等差中项,则
为等差中项,则![]() ,即
,即![]() ,化简得:
,化简得: ![]() ,
,
解得![]() ;
; ![]() ; 9分
; 9分
综上可得,满足要求的实数![]() 有且仅有一个,
有且仅有一个, ![]() ; 10分
; 10分
(3)![]() 则
则![]() ,
,
![]() ,
, ![]() , 12分
, 12分
当![]() 是偶数时,
是偶数时,
![]()
![]()
![]() ,
,
当![]() 是奇数时,
是奇数时,
![]()
![]()
![]()
![]()
![]() ,
, ![]() 也适合上式, 15分
也适合上式, 15分
综上可得, ![]()
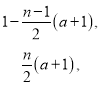
![]() . 16分
. 16分

 智能训练练测考系列答案
智能训练练测考系列答案【题目】如图,A,B,C是椭圆M:![]() 上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
上的三点,其中点A是椭圆的右顶点,BC过椭圆M的中心,且满足AC⊥BC,BC=2AC。
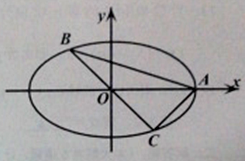
(1)求椭圆的离心率;
(2)若y轴被△ABC的外接圆所截得弦长为9,求椭圆方程。
【题目】在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2,…,6)的同学所得成绩,且前5位同学同学的成绩如表:
n | 1 | 2 | 3 | 4 | 5 |
x0 | 70 | 76 | 72 | 70 | 72 |
(1)求第6位同学的成绩x6及这6位同学成绩的标准差s;
(2)若从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间[68,75)中的概率.