题目内容
圆 内有一点
内有一点 ,
, 为过点
为过点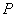 且倾斜角为
且倾斜角为 的弦,
的弦,
(1)当 =1350时,求
=1350时,求 ;
;
(2)当弦 被点
被点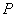 平分时,求出直线
平分时,求出直线 的方程;
的方程;
(3)设过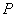 点的弦的中点为
点的弦的中点为 ,求点
,求点 的坐标所满足的关系式.
的坐标所满足的关系式.

解:(1)过点 做
做 于
于 ,连结
,连结 ,
,
当 =1350时,直线
=1350时,直线 的斜率为-1,故直线
的斜率为-1,故直线 的方程x+y-1=0,
的方程x+y-1=0,
∴OG=d= ,
,
又∵r= ,∴
,∴ ,
,
∴  ,
,
(2)当弦 被
被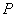 平分时,
平分时, ,此时KOP=
,此时KOP= ,
,
∴ 的点斜式方程为
的点斜式方程为 .
.
(3)解法一:设 的中点为
的中点为 ,
, 的斜率为K,
的斜率为K, ,则
,则 ,
,
消去K,得: ,当
,当 的斜率K不存在时也成立,故过点
的斜率K不存在时也成立,故过点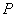 的弦的中点的轨迹方程为:
的弦的中点的轨迹方程为: .
.
解法二:设 的中点为
的中点为 ,则
,则
当OM的斜率和AB斜率都存在时:则

当OM斜率不存在时点M为(0,2)满足上式,
当AB斜率不存在时点M为(-1,0)亦满足上式,
所以M点的轨迹为 。
。

练习册系列答案
相关题目
 ,
, ,和圆C:
,和圆C:
 的位置关系是“平行相交”,则b的取值范围为
的位置关系是“平行相交”,则b的取值范围为 B.
B.  C.
C.  D.
D. 
 的直线,将圆形区域
的直线,将圆形区域 分两部分,使得这两部分的面积之差最大,则该直线的方程为( )
分两部分,使得这两部分的面积之差最大,则该直线的方程为( ) B.
B. C.
C. D.
D.
 与圆
与圆 ,过动点
,过动点 分别作圆
分别作圆 、圆
、圆 的切线
的切线 、
、 、
、 分别为切点),若
分别为切点),若 ,则
,则 的最小值是 .
的最小值是 . 是
是 的( )
的( ) 且
且 ,则
,则 =
=  (k<0)的定义域为B.
(k<0)的定义域为B. ≤λ恒成立,则λ的取值范围是________.
≤λ恒成立,则λ的取值范围是________.