题目内容
若函数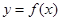 的导函数在区间
的导函数在区间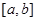 上是增函数,则函数
上是增函数,则函数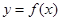 在区间
在区间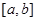 上的图象可能是( )
上的图象可能是( )
A
解析试题分析:根据题意,由于函数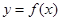 的导函数在区间
的导函数在区间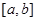 上是增函数,函数
上是增函数,函数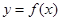 在区间
在区间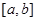 上的图象对于A,递增,的导数值从小的正数开始增大,成立,对于B,由于函数递增,导数的值逐渐减小,对于C,导数值不变,对于D,导数值先增大再减小,故选A.
上的图象对于A,递增,的导数值从小的正数开始增大,成立,对于B,由于函数递增,导数的值逐渐减小,对于C,导数值不变,对于D,导数值先增大再减小,故选A.
考点:导数的概念
点评:主要是考查了导数的几何意义的运用,属于基础题。

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知函数f(x)=x3+2bx2+cx+1有两个极值点x1、x2,且x1∈[-2,-1],x2∈[1,2],则f(-1)的取值范围是 ( )
| A.[-,3] | B.[,6] | C.[3,12] | D.[-,12] |
已知函数 的定义域为
的定义域为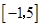 ,部分对应值如下表.
,部分对应值如下表.
 的导函数
的导函数 的图象如图所示.
的图象如图所示.
下列关于函数 的命题:①函数
的命题:①函数 在
在 是减函数;
是减函数;
②如果当 时,
时, 的最大值是2,那么
的最大值是2,那么 的最大值为4;
的最大值为4;
③当 时,函数
时,函数 有4个零点.
有4个零点.
其中真命题的个数是
| A.0个 | B.3个 | C. 2个 | D.1个 |
对于R上的可导的任意函数 ,若满足
,若满足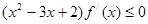 ,则函数
,则函数 在区间
在区间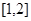 上必有( )
上必有( )
A. | B.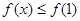 |
C.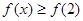 | D.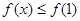 或 或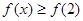 |
若实数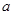 、
、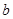 、
、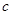 、
、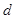 满足
满足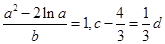 ,则
,则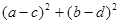 的最小值 为 ( )
的最小值 为 ( )
A.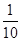 | B.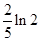 | C.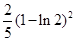 | D.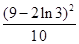 |
设函数 及其导函数
及其导函数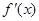 都是定义在R上的函数,则“
都是定义在R上的函数,则“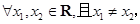
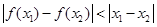 ”是“
”是“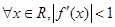 ”的
”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数f(x)=x2+2x+blnx,若函数f(x)在(0,1)上单调,则实数b的取值范围是
| A.b≥ 0 | B.b<-4 | C.b≥0或b≤-4 | D.b>0或b<-4 |
 具有下列特征:
具有下列特征: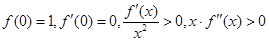 ,则
,则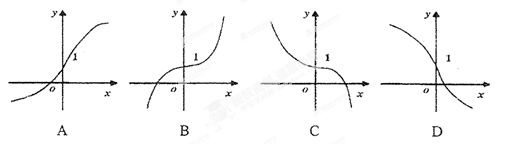
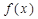 是定义在R上的奇函数,且
是定义在R上的奇函数,且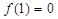 ,当
,当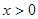 时,有
时,有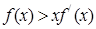 恒成立,则不等式
恒成立,则不等式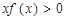 的解集为( )
的解集为( )