题目内容
(本小题满分12分)如图所示,在直三棱柱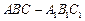 中,已知
中,已知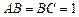 ,
,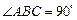 ,
,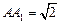 ,
,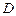 ,
,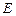 分别为
分别为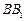 、
、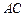 的中点.
的中点.
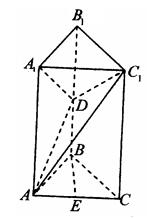
(I)证明: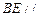 平面
平面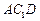 ;(II)求二面角
;(II)求二面角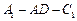 的大小.
的大小.
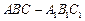 中,已知
中,已知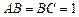 ,
,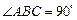 ,
,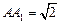 ,
,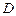 ,
,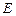 分别为
分别为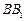 、
、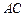 的中点.
的中点.
(I)证明:
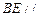 平面
平面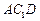 ;(II)求二面角
;(II)求二面角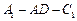 的大小.
的大小.  .
.(Ⅰ)证明:以 所在的直线为
所在的直线为 轴,
轴, 所在的直线为
所在的直线为 轴,
轴,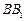 所在的直线为
所在的直线为 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,
, ,……2分
,……2分
设平面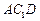 的一个法向量为
的一个法向量为 ,
,
则由 和
和 ,
, ,
,
取 ,
, ,
, ,所以法向量
,所以法向量 ,
,
又 ,
, ,
,
因为
 平面
平面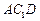 ,所以
,所以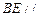 平面
平面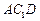 .……6分
.……6分


(另证:不建坐标系,取 的中点
的中点 ,连结
,连结 ,证明
,证明 )
)
(Ⅱ)解:由⑴可知,平面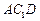 的法向量为
的法向量为 .又平面
.又平面 的法向量为
的法向量为 ,所以
,所以

 ,……10分
,……10分
由图可知,所求的二面角为锐角,所以二面角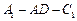 的大小为
的大小为 .……12分
.……12分
(另解:得用射影面积法求 ,
, 是
是 在面
在面 内的射影,利用关系式
内的射影,利用关系式 即可确定
即可确定 角).
角).
 所在的直线为
所在的直线为 轴,
轴, 所在的直线为
所在的直线为 轴,
轴,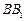 所在的直线为
所在的直线为 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,则
,则 ,
, ,
, ,
, ,
, ,
, ,
, ,……2分
,……2分设平面
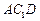 的一个法向量为
的一个法向量为 ,
,则由
 和
和 ,
, ,
,取
 ,
, ,
, ,所以法向量
,所以法向量 ,
,又
 ,
, ,
,因为

 平面
平面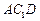 ,所以
,所以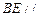 平面
平面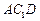 .……6分
.……6分


(另证:不建坐标系,取
 的中点
的中点 ,连结
,连结 ,证明
,证明 )
)(Ⅱ)解:由⑴可知,平面
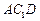 的法向量为
的法向量为 .又平面
.又平面 的法向量为
的法向量为 ,所以
,所以

 ,……10分
,……10分由图可知,所求的二面角为锐角,所以二面角
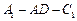 的大小为
的大小为 .……12分
.……12分(另解:得用射影面积法求
 ,
, 是
是 在面
在面 内的射影,利用关系式
内的射影,利用关系式 即可确定
即可确定 角).
角).
练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
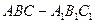 中,侧棱与底面垂直,
中,侧棱与底面垂直,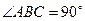 ,
,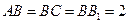 ,
, 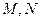 分别是
分别是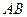 ,
,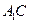 的中点.
的中点.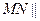 平面
平面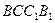 ;
; 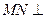 平面
平面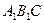 ;
;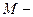

 中,侧面
中,侧面 与侧面
与侧面 均为边长为1
均为边长为1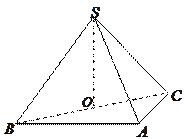
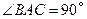 ,
,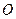 为
为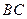 中点.
中点.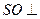 平面
平面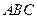 ;
;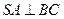 ;
;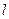 与曲线
与曲线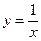 相切,分别求
相切,分别求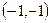 ;(2)
;(2)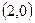 ;(3)
;(3)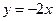 ;
;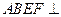 平面
平面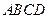 ,四边形
,四边形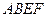 与
与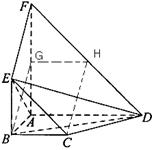
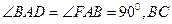
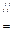
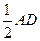 ,
,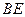
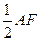 ,
,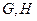 分别为
分别为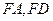 的中点
的中点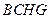 是平行四边形;
是平行四边形;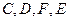 四点是否共面?为什么?
四点是否共面?为什么?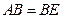 ,证明:平面
,证明:平面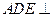 平面
平面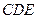 ;
;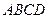 为矩形,
为矩形,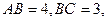 且
且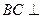 平面
平面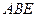 ,
,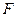 为
为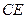 上的点,且
上的点,且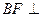 平面
平面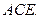
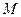 为线段
为线段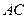 的中点,点
的中点,点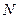 为线段
为线段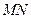 ∥平面
∥平面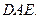

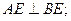
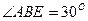 时,求三棱锥
时,求三棱锥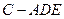 的体积。
的体积。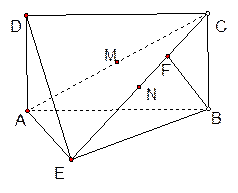
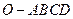 中,底面
中,底面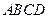 四边长为1的菱形,
四边长为1的菱形,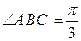 ,
,  ,
, 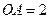 ,
,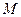 为
为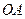 的中点,
的中点,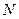 为
为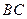 的中点,求异面直线OC与MN所成角的余弦值。
的中点,求异面直线OC与MN所成角的余弦值。
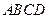 和
和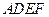 所在平面互相垂直,设
所在平面互相垂直,设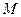 、
、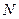 分别是
分别是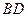 和
和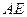 的中点,那么①
的中点,那么① 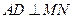 ;②
;② 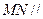 面
面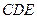 ;③
;③ 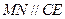 ;④
;④ 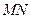 、
、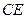 异面
异面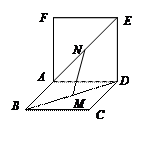
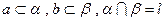 ,则l与a、b的位置关系一定是
,则l与a、b的位置关系一定是