题目内容
已知f（x）=logax在[3，+∞）上恒有|f（x）|＞1，求a的取值范围．
解：当a＞1时，∵x∈[3，+∞），∴y=f（x）=logax＞0，
由|f（x）|＞1，得logax＞1=logaa，∴a＜x对任意x∈[3，+∞）恒成立．
于是：1＜a＜3．
当0＜a＜1时，∵x∈[3，+∞），∴y=f（x）=logax＜0，
由|f（x）|＞1，得
，∴a＜x对任意x∈[3，+∞）恒成立．
于是：
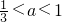． 综之：
．
分析：当a＞1时，不等式即 logax＞1=logaa，故a＜x对任意x∈[3，+∞）恒成立，得到1＜a＜3，当0＜a＜1时，不等式即，故a＜x对任意x∈[3，+∞）恒成立，故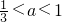，将两种情况下求得的a的取值范围再取并集．
点评：本题考查绝对值不等式的解法，对数函数的单调性及特殊点，体现了分类讨论的数学思想．
由|f（x）|＞1，得logax＞1=logaa，∴a＜x对任意x∈[3，+∞）恒成立．
于是：1＜a＜3．
当0＜a＜1时，∵x∈[3，+∞），∴y=f（x）=logax＜0，
由|f（x）|＞1，得
，∴a＜x对任意x∈[3，+∞）恒成立．于是：
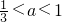． 综之：．分析：当a＞1时，不等式即 logax＞1=logaa，故a＜x对任意x∈[3，+∞）恒成立，得到1＜a＜3，当0＜a＜1时，不等式即
，故a＜x对任意x∈[3，+∞）恒成立，故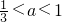，将两种情况下求得的a的取值范围再取并集．点评：本题考查绝对值不等式的解法，对数函数的单调性及特殊点，体现了分类讨论的数学思想．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
已知f（x）是定义在R上的奇函数，当x＞0时，f（x）=log
x，那么f（-
）的值是（ ）
| 1 |
| 4 |
| 1 |
| 2 |
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |