题目内容
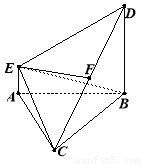
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,M是棱PD的中点,且PA=AB=AC=2,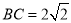 .
.

(1)求证:CD⊥平面PAC;
(2)求二面角M-AB-C的大小;
(3)如果N是棱AB上一点,且直线CN与平面MAB所成角的正弦值为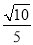 ,求
,求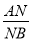 的值.
的值.
(1)证明见解析;(2)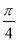 ;(3)1.
;(3)1.
【解析】
试题分析:(1)利用勾股定理与线面垂直的判定与性质进行证明;(2)建立适当的空间直角坐标系,利用空间向量求二面角;(3)设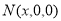 ,利用空间向量求线面角,得到关于
,利用空间向量求线面角,得到关于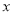 的方程,解方程即可求解.
的方程,解方程即可求解.
试题解析:(1)连结AC.

因为在△ABC中,
AB= AC=2,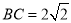 ,
,
所以  ,
,
所以 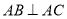 .
.
因为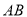 ∥
∥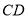 ,
,
所以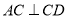 .
.
又因为 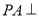 底面
底面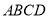 ,
,
所以 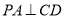 .
.
因为 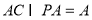 ,
,
所以 CD⊥平面PAC. 4分
(2)如图建立空间直角坐标系,

则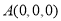 ,
,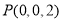 ,
,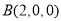 ,
,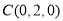 ,
,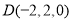 .
.
因为 M是棱PD的中点,
所以 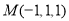 .
.
所以 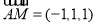 ,
,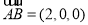 .
.
设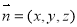 为平面MAB的法向量,
为平面MAB的法向量,
所以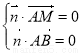 ,
,
即 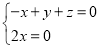 ,
,
令 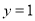 ,则
,则 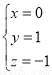 ,
,
所以平面MAB的法向量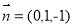 .
.
因为 PA⊥平面ABCD,
所以 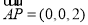 是平面ABC的一个法向量.
是平面ABC的一个法向量.
所以 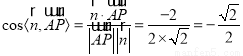 .
.
因为二面角M-AB-C 为锐二面角,
所以二面角M-AB-C的大小为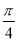 . 10分
. 10分
(3)因为N是在棱AB上一点,所以设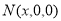 ,
,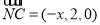 .
.
设直线CN与平面MAB所成角为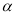 ,
,

因为平面MAB的法向量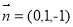 ,
,
所以
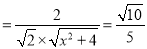 .
.
解得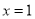 ,即
,即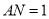 ,
, ,所以
,所以 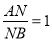 .
.
考点:1.线面垂直的判定定理;2.利用空间向量求线面角与二面角.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
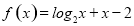 的零点所在的区间是( )
的零点所在的区间是( ) ,
,  ,则
,则 .
. 上单调递减的是( )
上单调递减的是( ) B.
B. C.
C. D.
D.
 且
且 的最大值是10,则k的值是 .
的最大值是10,则k的值是 . (b>0且b≠1)的图象如图所示,那么函数
(b>0且b≠1)的图象如图所示,那么函数 的图象可能是
的图象可能是

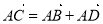 ”是“ABCD是平行四边形”的( )
”是“ABCD是平行四边形”的( )