题目内容
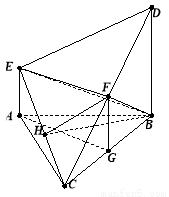
(本题满分15分)如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
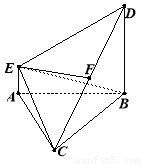
(Ⅰ)若F是线段CD的中点,证明:EF⊥面DBC;
(Ⅱ)求二面角D-EC-B的平面角的余弦值.
(1)利用线面垂直判定定理证明,(2)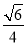
【解析】
试题分析:取BC的中点G,连接AG、FG,利用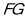 为三角形
为三角形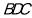 的中位线,
的中位线,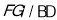 ,
,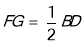 ,说明四边形
,说明四边形 是平行四边形,因此
是平行四边形,因此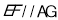 ,问题转化为证明
,问题转化为证明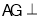 平面
平面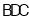 ,证明线面垂直,只需寻求线线垂直,因三角形ABC为等边三角形,则
,证明线面垂直,只需寻求线线垂直,因三角形ABC为等边三角形,则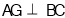 ,又DB⊥平面ABC,则
,又DB⊥平面ABC,则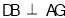 ,问题得以解决,第二步首先找出二面角,连接
,问题得以解决,第二步首先找出二面角,连接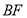 ,过
,过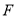 在面
在面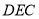 内作
内作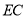 的垂线,垂足为
的垂线,垂足为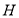 连接
连接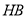 .因为
.因为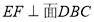 ,
,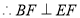 ,在三角形DBC中,
,在三角形DBC中,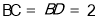 ,
,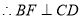 ,
,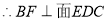 所以易证得
所以易证得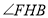 为二面角D-EC-B的平面角,在直角三角形
为二面角D-EC-B的平面角,在直角三角形 中,求出
中,求出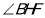 的余弦;
的余弦;
试题解析:(ⅰ)证明:取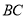 的中点
的中点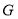 ,连接
,连接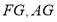
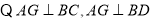
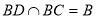
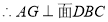 又因为
又因为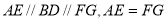
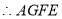 为平行四边形,
为平行四边形,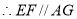
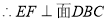 .
.
(ⅱ)连接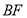 ,过
,过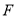 在面
在面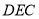 内作
内作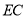 的垂线,垂足为
的垂线,垂足为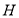 ,连接
,连接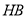 .因为
.因为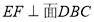 ,
,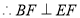
又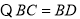
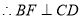 ,
,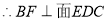 所以易证得
所以易证得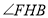 为二面角D-EC-B的平面角;
为二面角D-EC-B的平面角;
在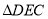 中,
中,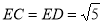
 所以易求得
所以易求得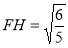 ,在直角
,在直角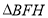 中,
中,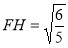 ,
,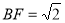 ,
,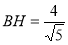 ,
, ,
,
所以二面角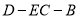 的平面角的余弦值为
的平面角的余弦值为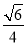
考点:1.线面垂直的判定;2.求二面角;

练习册系列答案
相关题目
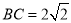 .
. 
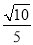 ,求
,求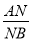 的值.
的值.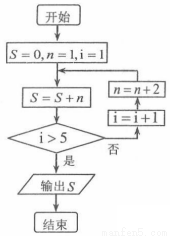
 ,值域为 ,不等式
,值域为 ,不等式 的解集为 .
的解集为 . 满足:
满足: ,则数列
,则数列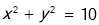 ,
, 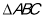 内接于此圆,
内接于此圆,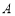 点的坐标
点的坐标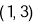 .若
.若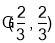 ,则线段
,则线段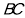 的中点坐标为 ,直线
的中点坐标为 ,直线 ,
,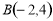 ,
,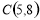 ,若线段
,若线段 和
和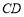 有相同的中垂线,则点
有相同的中垂线,则点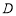 的坐标是
的坐标是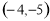 B.
B.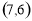 C.
C.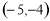 D.
D.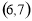
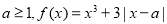 ,若函数
,若函数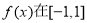 上的最大值和最小值分别记为
上的最大值和最小值分别记为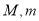 ,则
,则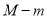 的值为 ( )
的值为 ( )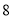 B.
B.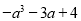 C.
C.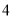 D.
D.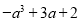
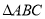 中,三内角
中,三内角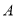 ,
,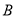 ,
,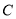 的对边分别为
的对边分别为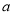 ,
,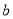 ,
,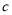 且
且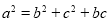 ,
,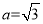 ,
,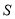 为
为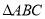 的面积,则
的面积,则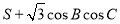 的最大值为 .
的最大值为 .