题目内容
6.已知数列{an}的前n项和为Sn.(Ⅰ)若数列{an}是等差数列,则满足a5=0,S1=2S2+8,求数列{an}的通项公式;
(Ⅱ)若2Sn=3an-1,证明数列{an}是等比数列,并求其前n项和Sn.
分析 (Ⅰ)设数列{an}的首项为a1,公差为d;从而可得a5=a1+4d=0,a1=2(2a1+d)+8,从而解得;
(Ⅱ)分类讨论,从而化简可得$\frac{{a}_{n}}{{a}_{n-1}}$=3,从而证明并求和.
解答 解:(Ⅰ)设数列{an}的首项为a1,公差为d;
则a5=a1+4d=0,a1=2(2a1+d)+8,
解得,a1=-$\frac{16}{5}$,d=$\frac{4}{5}$;
故an=-$\frac{16}{5}$+(n-1)$\frac{4}{5}$=$\frac{4}{5}$n-4;
(Ⅱ)证明:∵2Sn=3an-1,
①当n=1时,2S1=3a1-1,
解得,a1=1,
②当n≥2时,2Sn=3an-1,2Sn-1=3an-1-1,
故2an=3an-3an-1,
故$\frac{{a}_{n}}{{a}_{n-1}}$=3,
故数列{an}是以1为首项,3为公比的等比数列,
故Sn=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}$(3n-1).
点评 本题考查了等差数列与等比数列的应用及分类讨论的思想应用,同时考查了方程思想的应用.

练习册系列答案
相关题目
16.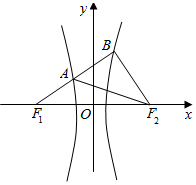 已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
 已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )
已知F1,F2分别为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点,若存在过F1的直线分别交双曲线C的左、右支于A,B两点,使得∠BAF2=∠BF2F1,则双曲线C的离心率e的取值范围是( )| A. | (3,+∞) | B. | (1,2+$\sqrt{5}$) | C. | (3,2+$\sqrt{5}$) | D. | (1,3) |
14.若实数x,y满足不等式组$\left\{\begin{array}{l}x+3y-3≤0\\ x-y+1≥0\\ y≥1\end{array}\right.$,则z=2|x|+y的取值范围是( )
| A. | [-1,3] | B. | [1,3] | C. | [-1,11] | D. | [-5,11] |
1.已知命题p:若a<1,则a2<1,下列说法正确的是( )
| A. | 命题p是真命题 | B. | 命题p的逆命题是真命题 | ||
| C. | 命题p的否命题是:若a<1,则a2≥1 | D. | 命题p的逆否命题是:若a2≥1,则a<1 |
18.已知复数w满足w-1=(1+w)i(i为虚数单位),则w=( )
| A. | 1-i | B. | -i | C. | -1+i | D. | i |
15.“a>1”是当“0<x≤2时,2-2x≥logax成立”的( )
| A. | 必要不充分条件 | B. | 充分不必要条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
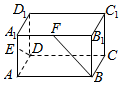 如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )
如图所示的长方体中,$AB=2\sqrt{6},AD=\sqrt{5},C{C_1}=2\sqrt{3},E,F$分别为AA1,A1B1的中点,则异面直线DE,BF所成角的大小为( )