题目内容
11.甲决定在某日0时至24时内随机向某网站发布一则信息,该网站将这则信息保留4小时,乙在这一天0时至24时内随机到此网站的同一网页浏览2小时,则乙能看到甲发布信息的概率为$\frac{43}{144}$.分析 设甲在x时发布信息,则在x时至x+4时网站保留此信息,乙y时到此网站的同一网页浏览2小时,$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,此区域的面积=24×24=576能看到甲发布的信息,则x-2≤y≤x+6且$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,此区域的面积=576-$\frac{1}{2}×22×22$-$\frac{1}{2}$×18×18=172,利用面积比,即可求出乙能看到甲发布信息的概率.
解答 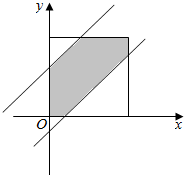 解:设甲在x时发布信息,则在x时至x+4时网站保留此信息,乙y时到此网站的同一网页浏览2小时,$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,此区域的面积=24×24=576
解:设甲在x时发布信息,则在x时至x+4时网站保留此信息,乙y时到此网站的同一网页浏览2小时,$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,此区域的面积=24×24=576
能看到甲发布的信息,则x-2≤y≤x+6且$\left\{\begin{array}{l}{0≤x≤24}\\{0≤y≤24}\end{array}\right.$,此区域的面积=576-$\frac{1}{2}×22×22$-$\frac{1}{2}$×18×18=172,
∴乙能看到甲发布信息的概率为$\frac{172}{576}$=$\frac{43}{144}$.
故答案为:$\frac{43}{144}$.
点评 本题考查几何概型,考查面积的计算,确定区域是关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
6.设f(x)=ax2+bx+c(a>0)满足f(1+x)=f(1-x),则f(2x)与f(3x)的大小关系为( )
| A. | f (3x)≥f (2x) | B. | f (3x)≤f (2x) | C. | f (3x)<f (2x) | D. | 不确定 |
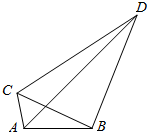 如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.
如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.