题目内容
证明对于任意实数t,复数z=
证明:r=![]() ,为证对于任意实数t有r≤
,为证对于任意实数t有r≤![]() ,
,
只要证|cost|+|sint|≤![]() 即可.
即可.
(1)当kπ≤t≤kπ+![]() (k∈Z)时,则sint·cost≥0,依推论1,|cost|+|sint|=|sint+cost|=
(k∈Z)时,则sint·cost≥0,依推论1,|cost|+|sint|=|sint+cost|=![]() |sin(t+
|sin(t+![]() )|≤
)|≤![]()
(2)当kπ+![]() <t<(k+1)π(k∈Z)时,sint·cost<0,sint·(-cost)>0,依推论1,|cost|+|sint|=|-cost|+|sint|=|sint-cost|=
<t<(k+1)π(k∈Z)时,sint·cost<0,sint·(-cost)>0,依推论1,|cost|+|sint|=|-cost|+|sint|=|sint-cost|=![]() |sin(t-
|sin(t-![]() )|≤
)|≤![]() .
.
总之,对于任意实数t,有|cost|+|sint|≤![]() 成立,即有r≤
成立,即有r≤![]() 成立.
成立.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
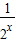 .
.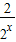 ,求x的值;
,求x的值;