题目内容

10．已知点P（x，y）满足$\left\{\begin{array}{l}{x-y≥-1}\\{x+y≤3}\\{y≥t}\end{array}\right.$，点Q（2，-1），若（$\overrightarrow{OP}•\overrightarrow{OQ}$）min=-3，则实数t=（　　）
A．-2B．-1C．$\frac{3}{4}$D．3

分析 首先画出平面区域，由（$\overrightarrow{OP}•\overrightarrow{OQ}$）min=-3即z=2x-y最小值为-3，结合可行域图象，得到关于t的等式解之．

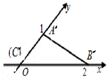
解答 解：不等式组表示的平面区域如图
由（$\overrightarrow{OP}•\overrightarrow{OQ}$）min=-3即z=2x-y最小值为-3，
结合图象可知，当直线过图中A（t-1，t）点时使z最小，
即2（t-1）-t=-3，解得t=-1；
故选：B．

点评 本题考查了简单线性规划问题中，参数的取值；关键是利用数形结合，直观的找到满足条件的点，求t．

练习册系列答案
相关题目
20．已知向量$\overrightarrow{a}$=（1，-1），A（0，4），B（n，t），C（t，ksinθ）θ∈[0，$\frac{π}{2}$]
（1）若$\overrightarrow{AB}⊥\overrightarrow{a}$，且$\frac{\sqrt{2}}{2}$|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$|（O为原点），求向量$\overrightarrow{AB}$；
（2）若向量$\overrightarrow{AC}$与向量$\overrightarrow{a}$共线，求t关于θ的函数；
（3）求tsinθ取得最大值1（k≥2）时的$\overrightarrow{AC}$．
1．函数y=${∫}_{0}^{x}$costdt的导数是cosx．
18．若（a$\sqrt{x}$-$\frac{1}{\root{3}{x}}$）5展开式中的常数项为-40，则a=±2．
5．已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）求函数f（x）的图象上的三点M，N，P的横坐标分别为-1，1，5，求sin∠MNP的值；
（3）若对任意的x1，x2∈[1，2]，关于m的不等式|f（x1）-f（x2）|≤-m2+2m+4恒成立，求实数m的取值范围．
15．在四棱锥P-ABCD中，四条侧棱长均为2，底面ABCD为正方形，E为PC的中点．若异面直线PA与BE所成的角为45°．则该四锥的体积是$\frac{2\sqrt{3}}{3}$．
3．已知动圆P与圆${F_1}：{（x+3）^2}+{y^2}=81$相切，且与圆${F_2}：{（x-3）^2}+{y^2}=1$相内切，记圆心P的轨迹为曲线C，求曲线C的方程．
20．△ABC的斜二测直观图△A′B′C′如图所示，则△ABC的面积为（　　）
A．1B．2C．$\frac{{\sqrt{2}}}{2}$D．$\sqrt{2}$
1．已知直线l在x轴上的截距为3，在y轴上的截距为-2，则l的方程为（　　）
A．3x-2y-6=0B．2x-3y+6=0C．2x-3y-6=0D．3x-2y+6=0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网