题目内容
8.已知等差数列{an}满足:a1=2,且a1,a3,a13成等比数列.(Ⅰ)求数列{an}的通项公式.
(Ⅱ)记Sn为数列{an}的前项n和,是否存在正整数n,使得Sn>40n+600?若存在,求n的最小值;若不存在,说明理由.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用等差数列求和公式与不等式的解法即可得出.
解答 解:(1)设数列{an}公差为d,由$a_3^2={a_1}{a_{13}}得{({2+2d})^2}=2({2+12d})$…(2分)
解得d=0或d=4,…(4分)
故an=2或an=4n-2; …(6分)
(2)当an=2时,Sn=2n…(7分)Sn=2n<40n+600.不存在正整数n,使得Sn>40n+600…(8分)
当an=4n-2时,${S_n}=2{n^2}$…(9分)
由2n2>40n+600解得n>30或n<-10(舍去)
此时存在正整数n使得Sn>40n+600.且n的最小值为31.…(11分)
综上,当an=2时,不存在正整数n,使得Sn>40n+600
当an=4n-2时,存在正整数n使得Sn>40n+600.且n的最小值为31.…(12分)
点评 本题考查了数列递推关系、等比数列与等差数列的通项公式与求和公式、不等式的解法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
6.已知定义在[1,+∞)上的函数f(x)=$\left\{\begin{array}{l}{4-8|x-\frac{3}{2}|,1≤x≤2}\\{\frac{1}{2}f(\frac{x}{2}),x>2}\end{array}\right.$,函数y=xf(x)-6在[1,16]内零点之和为( )
| A. | $\frac{45}{2}$ | B. | 23 | C. | $\frac{47}{2}$ | D. | 24 |
20.已知集合A={x|(5x+1)(2-x)<0},B={x|x<4},则A∩B等于( )
| A. | (-∞,4) | B. | (-$\frac{1}{5}$,2) | C. | (2,4) | D. | (-∞,-$\frac{1}{5}$)∪(2,4) |
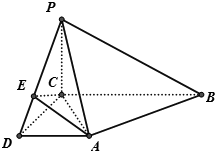 如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.
如图,在四棱锥P-ABCD中,AD∥BC,且BC=2,AD=CD=PC=1,AD⊥CD,PC⊥平面ABCD,点E在棱PD上,且PE=2ED.