题目内容
2.已知正方体ABCD-A1B1C1D1中,AB=2,E、F分别是CC1、D1A1的中点,求点A到EF的距离.分析 求出△AEF中,AF=$\sqrt{5}$,AE=3,EF=$\sqrt{6}$,利用余弦定理可得cos∠EAF,进而可求sin∠EAF,再利用等面积,即可求出点A到EF的距离.
解答 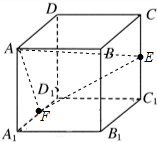 解:由题意,△AEF中,AF=$\sqrt{5}$,AE=3,EF=$\sqrt{6}$,
解:由题意,△AEF中,AF=$\sqrt{5}$,AE=3,EF=$\sqrt{6}$,
∴cos∠EAF=$\frac{9+5-6}{2×3×\sqrt{5}}$=$\frac{4}{3\sqrt{5}}$,
∴sin∠EAF=$\frac{\sqrt{29}}{3\sqrt{5}}$,
设点A到EF的距离为h,则由等面积可得$\frac{1}{2}×3×\sqrt{5}×\frac{\sqrt{29}}{3\sqrt{5}}$=$\frac{1}{2}×\sqrt{6}h$,
∴h=$\frac{\sqrt{174}}{6}$.
点评 本题考查点A到EF的距离,考查余弦定理,正确求面积是关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
11.某研究机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
由表中数据,求得线性回归方程为$\widehaty=\frac{4}{5}$$x+\widehata$,若某儿童的记忆能力为12时,则他的识图能力为( )
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 9.2 | B. | 9.5 | C. | 9.8 | D. | 10 |
 如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].
如图,在△AOB中,∠AOB=$\frac{π}{2}$,∠BAO=$\frac{π}{6}$,AB=4,D为线段BA的中点.△AOC由△AOB绕直线AO旋转而成,记∠BOC=θ,θ∈(0,$\frac{π}{2}$].