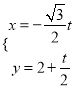��Ŀ����
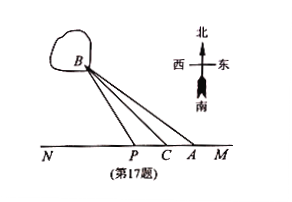
����Ŀ����2017��һģ����ͼ��ij���������۹���![]() Χ��ֱ�������Σ�����ֱ�DZ�
Χ��ֱ�������Σ�����ֱ�DZ�![]() ��
��
б��![]() �����мס��ҡ�����λС���ѷֱ���
�����мס��ҡ�����λС���ѷֱ���![]() �������Ϸ������λ
�������Ϸ������λ
�÷ֱ��Ϊ��![]() ��
��
��1�������Ҷ���ÿ����![]() ���ٶȴӵ�
���ٶȴӵ�![]() �����ڸ��ԵĴ���ϱ��ߣ����������һ��
�����ڸ��ԵĴ���ϱ��ߣ����������һ��
ʱ��ͣ���ұȼ׳�![]() ���ӳ��������ҳ���
���ӳ��������ҳ���![]() ���Ӻ����ʱ��������֮��ľ��룻
���Ӻ����ʱ��������֮��ľ��룻
��2����![]() ���ұ�֮��ľ����Ǽ���֮������
���ұ�֮��ľ����Ǽ���֮������![]() ������
������![]() ���뽫��
���뽫��
��֮��ľ���![]() ��ʾΪ
��ʾΪ![]() �ĺ������������֮�����С������
�ĺ������������֮�����С������
���𰸡�������
���������⣺��1���������![]() ��
��![]() ��
��
����![]() ��
��![]() ����
����![]() ������2��
������2��
����![]() �У������Ҷ����ã�
�У������Ҷ����ã�
![]() ��
��
��![]() .����6��
.����6��
�𣺼�������֮��ľ���Ϊ![]() m.����7��
m.����7��
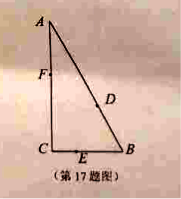
��2���������![]() ��
��![]() ��
��
��ֱ��������![]() �У�
��![]() ������9��
������9��
����![]() �У������Ҷ�����
�У������Ҷ�����![]() ����
����![]() ��
��
�� ��
��![]() ������12��
������12��
���Ե�![]() ʱ��
ʱ��![]() ����Сֵ
����Сֵ![]() .����13��
.����13��
������֮�����С����Ϊ![]() .����14��
.����14��

��ϰ��ϵ�д�
 â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
�����Ŀ