题目内容
12．若$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是两个不共线的单位向量，若$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$与k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$垂直，则实数k=1．分析 设$＜\overrightarrow{{e}_{1}}，\overrightarrow{{e}_{2}}＞$=θ∈（0，π）．由于$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$与k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$垂直，可得（$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$）•（k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$）=0，化为（k-1）（1-cosθ）=0，即可得出．
解答 解：设$＜\overrightarrow{{e}_{1}}，\overrightarrow{{e}_{2}}＞$=θ∈（0，π）．
∵$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$与k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$垂直，
∴（$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$）•（k$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$）=k${\overrightarrow{{e}_{1}}}^{2}$-${\overrightarrow{{e}_{2}}}^{2}$+（1-k）$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=k-1+（1-k）cosθ=0，
∴（k-1）（1-cosθ）=0，
∵$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是两个不共线的单位向量，
∴1-cosθ≠0，
∴k-1=0，解得k=1．
故答案为：1．
点评 本题考查了向量垂直与数量积的关系、向量共线，考查了推理能力与计算能力，属于中档题．
互动英语系列答案
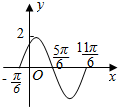如图是$y=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜\frac{π}{2}）$的图象，则其解析式为$y=2sin（x+\frac{π}{6}）$．